Nagu eelnevas kogesime, võib funktsiooni esitada mitmel erineval viisil. Järgnevas vaatleme funktsiooni põhilisi esitusviise.
1. VALEM EHK ANALÜÜTILINE ESITUS
Sel juhul on antud võrdus, mille kohaselt on x igale väärtusele võimalik arvutada y väärtust. Valemist nähtub, milliseid tehteid ja millises järjekorras tuleb argumendi väärtusega teha, et saada vastav funktsiooni väärtus. Kui näiteks funktsioon on antud valemiga y = x2 + 1, siis on iga reaalarvulise x jaoks selle valemi abil võimalik y arvutada.
Funktsioon võib olla esitatud ka mitme valemiga. Kahe valemiga esitatud funktsioon on näiteks (ehk y = |x|).
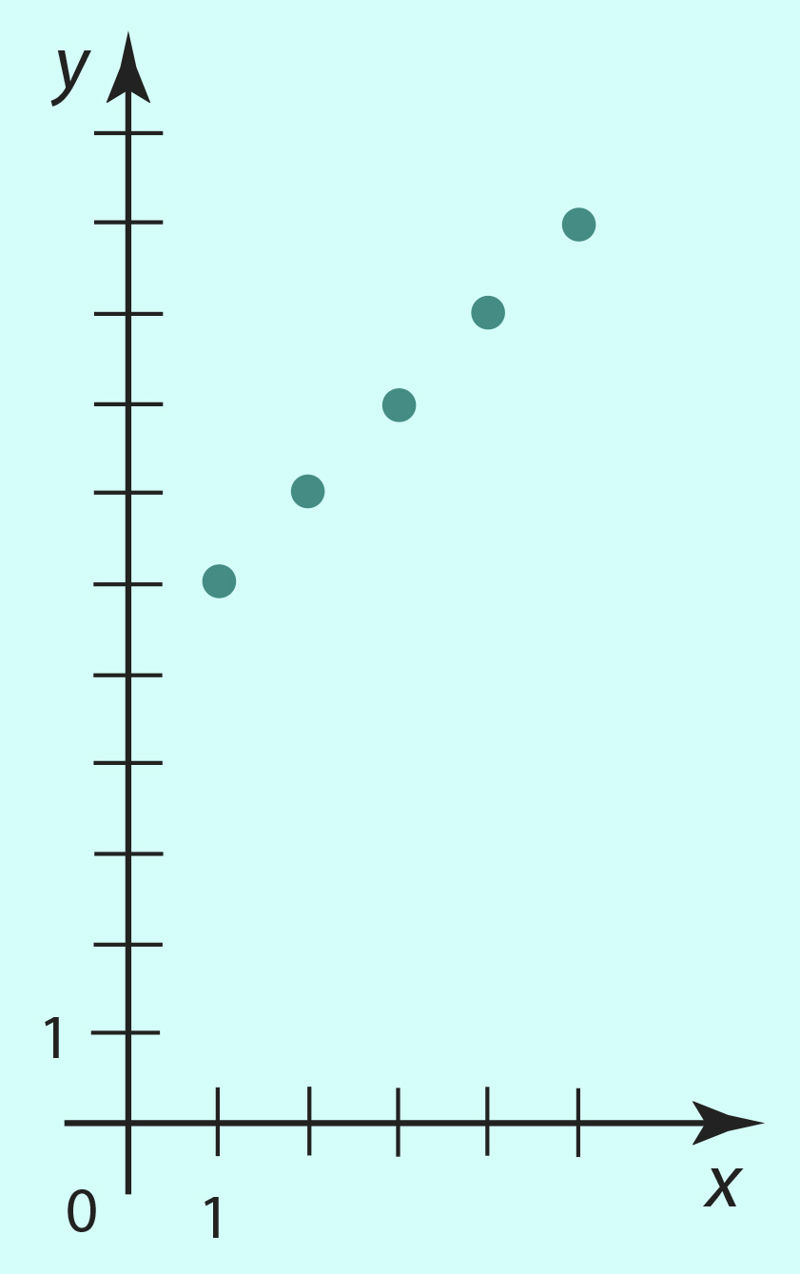
Joon. 2.24 |
||||||
2. GRAAFIK
Graafik võimaldab funktsiooni kujutada piltlikult. Graafikul on funktsiooni mitmed omadused selgemini nähtavad kui valemis. Funktsiooni f graafiku moodustavad tasandi need punktid, mille koordinaadid on (x; f (x)). Tavaliselt on funktsiooni graafikuks mingi joon, kuid mitte iga joon pole funktsiooni graafikuks. Funktsiooni graafikuks saab olla vaid selline joon, mille korral x igale väärtusele vastab vaid üks punkt sellel joonel.
Tavaliselt on koordinaatteljestikus võimalik kujutada vaid osa funktsiooni graafikust. Funktsiooni graafik võib koosneda kas üksikutest punktidest, pidevast joonest või mitmest pidevast joonest. Näiteks peatüki 2.9 näites 1 esitatud funktsiooni graafik koosneb 5 punktist (joonis 2.24). Praktikas leiavad laialdast kasutamist näiteks liikumise graafikud, kardiogrammid jne.
3. TABEL
Tabelis esitatakse ühes reas (või veerus) argumendi x väärtused, teises reas (veerus) sellele vastavad funktsiooni väärtused. Näiteks oli funktsioon esitatud tabelina ülesandes 439. Enne taskuarvutite võidukäiku kasutati arvutustes näiteks arvu ruudu (funktsiooni y = x2, x ∈ N), arvu kuubi ja ruutjuure tabeleid. Funktsiooni esitust tabelina kasutatakse tihti abivahendina funktsiooni graafiku joonestamisel, kui funktsioon on antud valemiga.
Mõnikord täiendatakse funktsiooni esitavat tabelit nii, et näidatakse nooltega, missugune element hulgast Y vastab igale elemendile hulgast X (joonis 2.25). Selline esitus võimaldab paremini näha, kas vastavus kahe hulga vahel on funktsioon või mitte. Funktsiooni puhul on oluline, et 1) argumendi igale väärtusele vastaks funktsiooni väärtus ja 2) et neid väärtusi oleks argumendi iga väärtuse jaoks vaid üks. Sel juhul peab hulga X iga elemendi juurest lähtuma vaid üks nool.
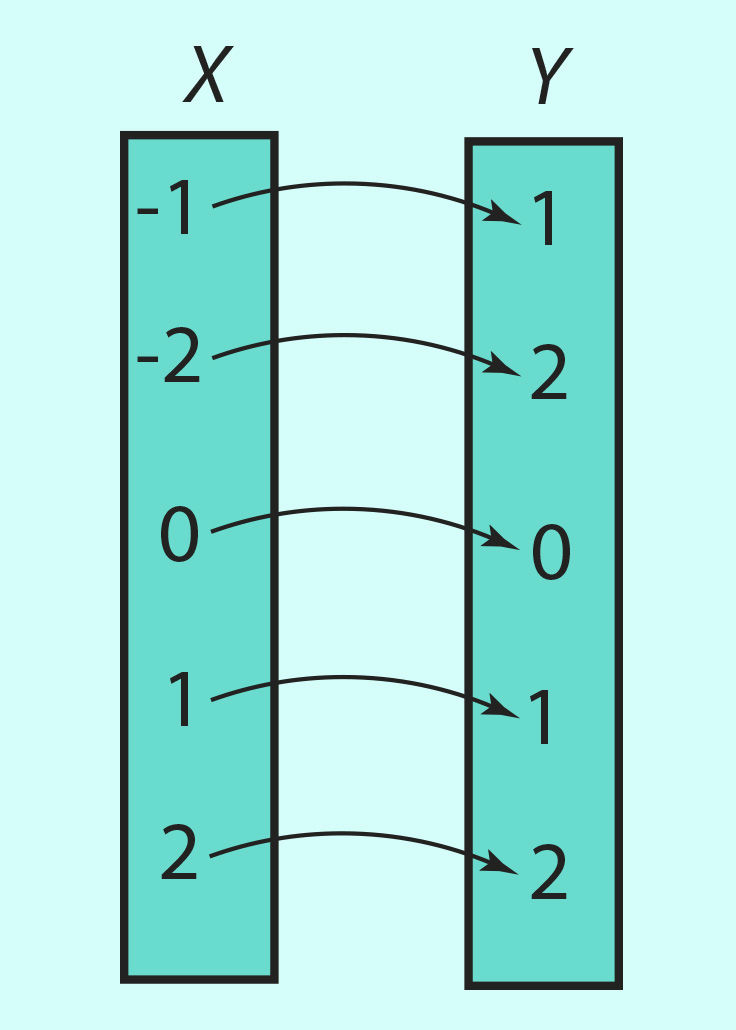
Joon. 2.25 |
||||||||
4. ARVUPAARID
Funktsiooni sellise esituse jaoks moodustame kõik võimalikud järjestatud arvupaarid, milles esimesel kohal on argumendi väärtus ja teisel kohal sellele vastav funktsiooni väärtus.
Näiteks olgu antud funktsioon y = |x|, kus X = {–2, –1, 0, 1, 2}. Selle funktsiooni võime esitada arvupaaride hulgana järgmiselt: {(–2; 2), (–1; 1), (0; 0), (1; 1), (2; 2)}.
Näide 1.
Joonisel 2.26 on esitatud funktsioon, sest igale väärtusele (harilikule murrule) hulgast X vastab ainult üks element (kümnendmurd) hulgast Y.
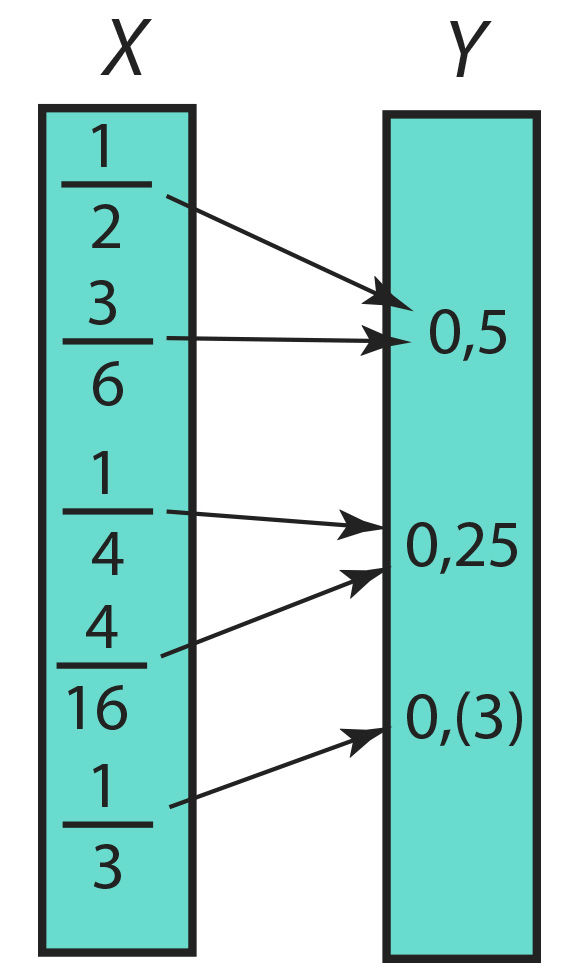 Joon. 2.26 | ||||||
Näide 2.
Kodumasinate müüja põhipalk on 1000 eurot kuus. Kui kuu läbimüük ületab 30 000 eurot, makstakse müüjale tasu 40% põhipalgast ja 2% läbimüügist. Leiame valemi müüja kuupalga y arvutamiseks sõltuvalt läbimüügist x.
Kuupalk on muutumatu, kui läbimüük ei ületa 30 000 eurot kuus. Kui x ∈ [0; 30 000], siis y = 1000.
Kui x > 30 000, siis y = 0,4 · 1000 + 0,02x = 400 + 0,02x.
Lühemalt võib selle esitada järgmiselt:
Selle funktsiooni graafik on kujutatud joonisel 2.27.
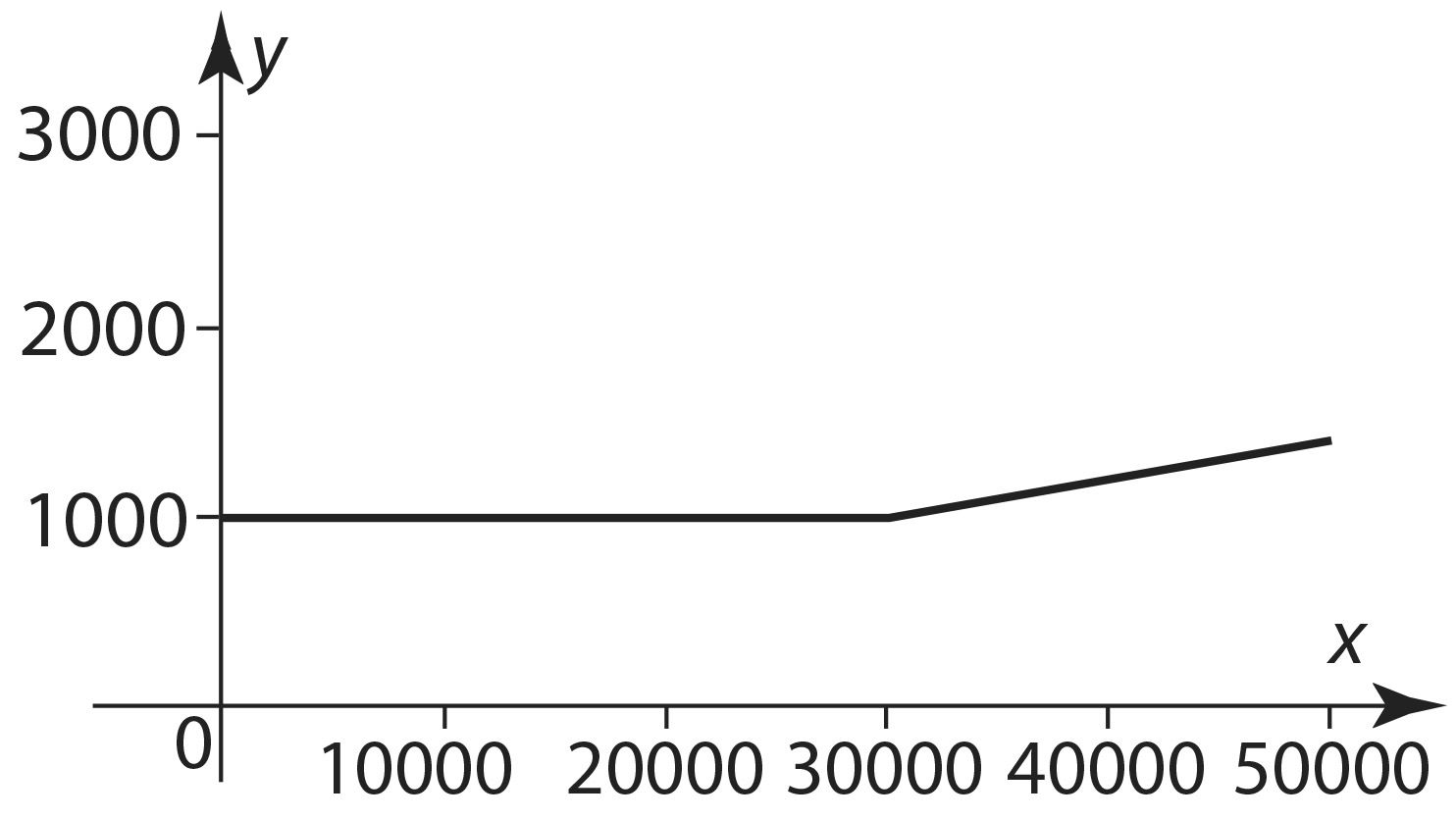
Näide 3.
Autofirma uuris auto pidurdustee pikkust sõltuvalt auto kiirusest ja sai järgmised tulemused:

Seos nende kahe suuruse vahel on funktsioon. Püüame esitatud andmete põhjal leida üldist valemit, mis võimaldaks leida auto pidurdustee pikkust s (meetrites) sõltuvalt auto kiirusest v (kilomeetrit tunnis). Kanname selleks kõigepealt vastavad punktid koordinaatteljestikku (joonis 2.28).
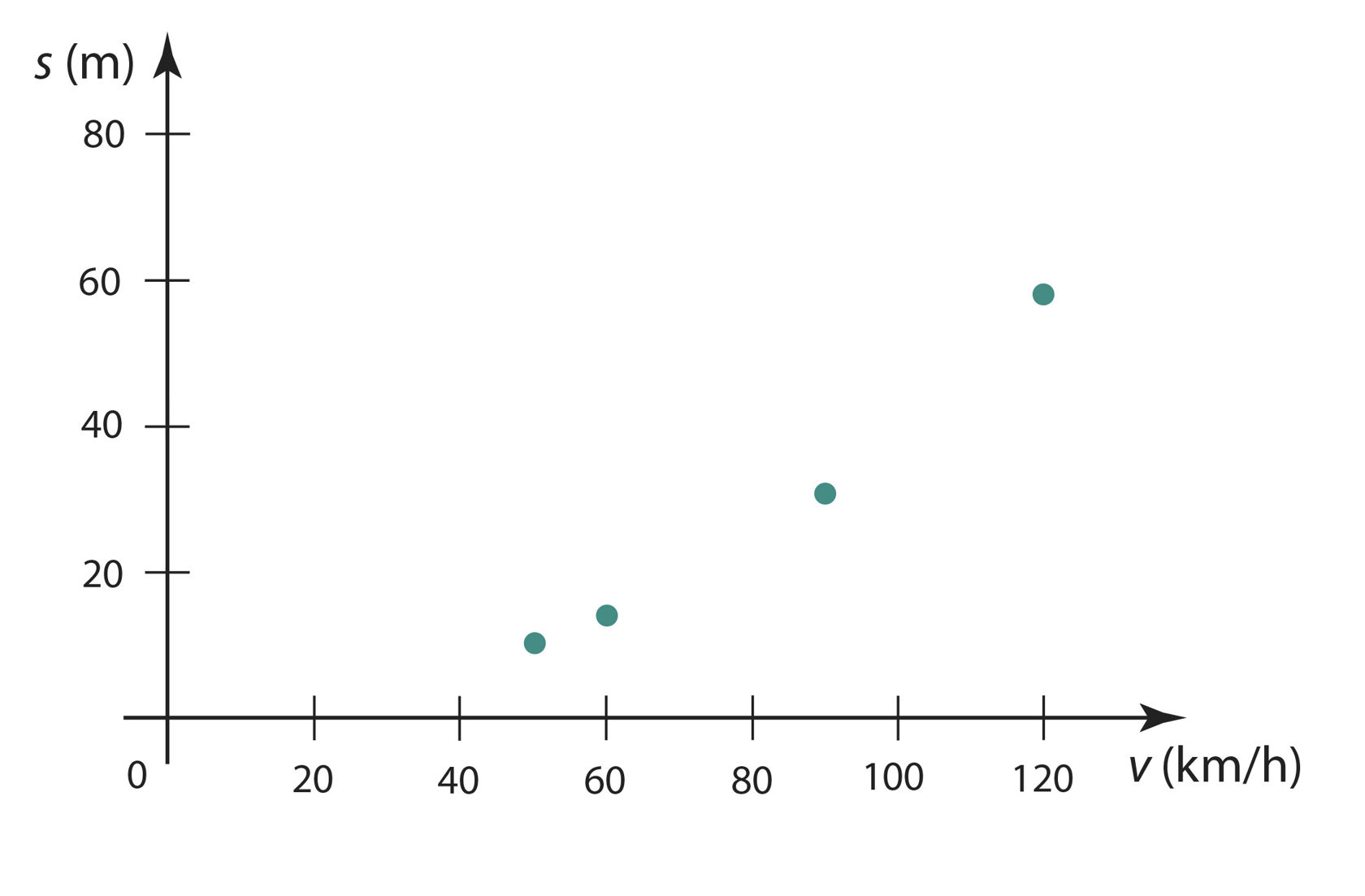 Joon. 2.28 | ||||||
Näeme, et need punktid ei asu ühel sirgel. Meile tuntud funktsioonidest on saadud graafik kõige enam sarnane paraboolile (ruutfunktsiooni graafikule). Et auto kiiruse 0 km/h puhul on ilmselt ka pidurdustee pikkus 0 m, siis läbib antud parabool koordinaatide alguspunkti. Sellise parabooli võrrand on y = ax2. Parameetri a väärtuse määrame meie tabeli andmete põhjal näiteks nii:
Selle valemi põhjal saame leida pidurdustee pikkuse auto igasuguse kiiruse puhul, samuti aga ka vastavalt pidurdustee pikkusele leida auto kiiruse. Näiteks, kui auto kiirus on 100 km/h, on pidurdustee 0,004 · 10 000 = 40 meetrit.
Ülesanded A
Ülesanne 442. Funktsiooni esitusviisid
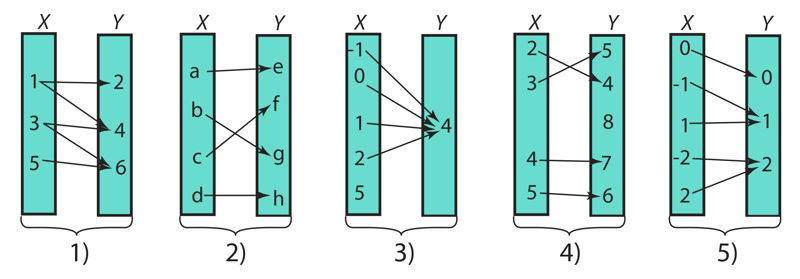
- 1)
- 2)
- 3)
- 4)
- 5)
Ülesanne 443. Funktsiooni esitusviisid
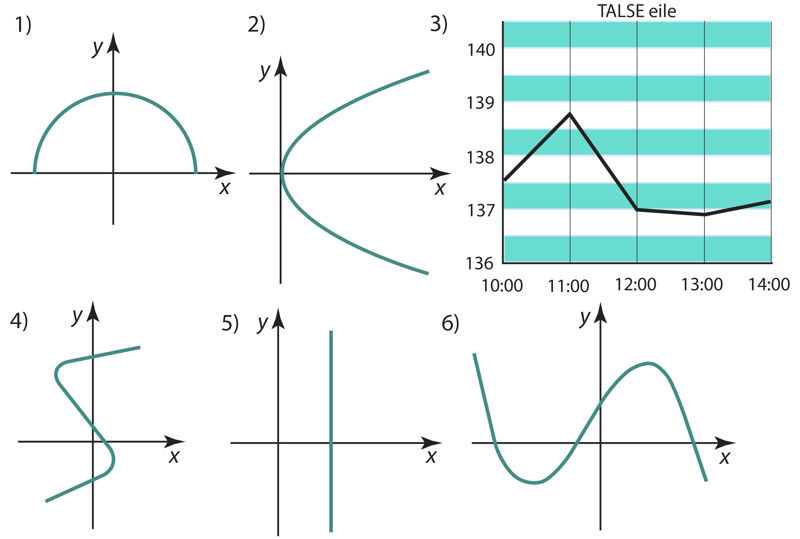
- 1)
- 2)
- 3)
- 4)
- 5)
- 6)
Ülesanne 444. Pidurdustee pikkus

- Leidke valem maastikuauto pidurdustee pikkuse s (meetrites) leidmiseks sõltuvalt auto kiirusest v (km/h).
Vastus. s = - Kui pikk on auto pidurdustee, kui auto sõidab kiirusega 80 km/h; 100 km/h?
Vastus. Kiirusel 80 km/h on pidurdustee pikkus m ja kiirusel 100 km/h m. - Kui kiiresti sõitis auto, kui pidurdustee pikkus oli 62,2 m; 24,5 m?
Vastus. Kui pidurdustee pikkus oli 62,2 m, siis kiirus oli km/h ja kui 24,5 m, siis km/h.
Ülesanne 445. Matkamine
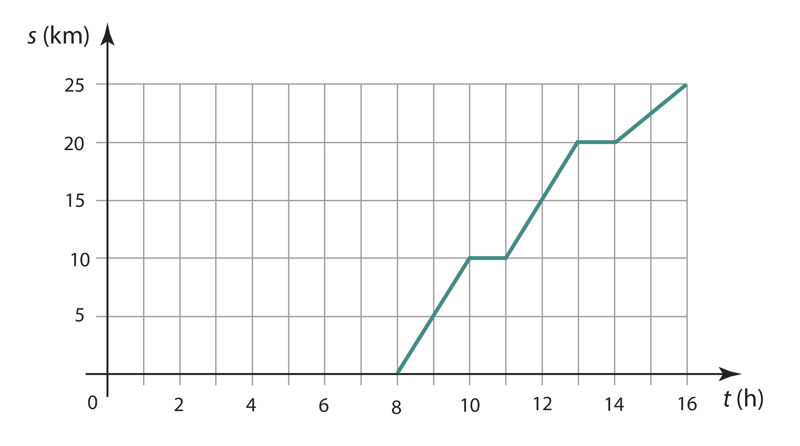
- Kui palju aega kulus kogu matkaks ja kui palju sellest puhkusteks?
Vastus. Kogu matkaks kulus h ja sellest puhkusteks h. - Mitu kilomeetrit läbis ta esimese tunni jooksul?
Vastus. Esimese tunni jooksul läbis ta km. - Kui palju aega kulus esimese 10 km ja kui palju viimase 10 km läbimiseks?
Vastus. Esimese 10 km läbimiseks kulus h ja viimase 10 km läbimiseks h. - Leidke vastava funktsiooni määramispiirkond X ja muutumispiirkond Y.
Vastus. X =; Y = .
Ülesanne 446. Koeraaed
S =
- Joonestage (arvutil) selle funktsiooni graafik, leidke määramis- ja muutumispiirkond.
Vastus. X =; Y = . - Leidke graafikult, missuguse pikkuse x korral on aia pindala suurim.
Vastus. Kui x = . - Milline saaks reaalselt olla aia lühema külje pikkus?
Vastus. Aia lühema külje pikkus saaks olla m kuni m.
Ülesanded B
Ülesanne 447. Funktsiooni graafik
Ülesanne 448. Karbi ruumala
V =
X =
Ülesanne 449. Limusiini rent
- Joonestage funktsiooni graafik.
- Kui suur on limusiini rent, kui läbisõit on 300 km?
Vastus. Siis on rent eurot.
Ülesanne 450. Suvila aken
C =
