Умножение многочленов

Ты уже знаешь, что при умножении двух двучленов нужно каждый член одного двучлена умножить на каждый член другого двучлена и полученные произведения сложить (см. § 1.6). Распределительный закон умножения позволяет так же умножать любые два многочлена.

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Например, перемножив двучлен а + b и трехчлен x + y + z, получим:

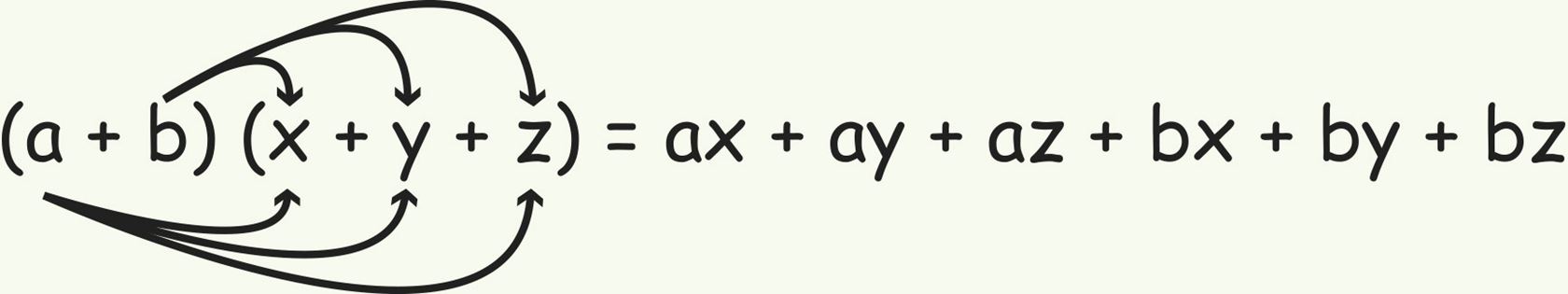Если в полученном многочлене есть подобные, то нужно выполнить их приведение.

(2a – b)(a² – 2a + b) =

= 2a · a² – 2a · 2a + 2a · b – b · a² + b · 2a – b · b =

= 2a³ – 4a² + 2ab – a²b + 2ab – b² =

= 2a³ – a²b – 4a² + 4ab – b²

Lisää aiheesta

Упражнения A

(m + n)(a + b + c) =

(c – d + 2)(a + b) =

(u – v)(f – g – h) =

(a + c – d)(s – t) =

(a – y)(b + c + x) =

(b – 2)(x – y + 1) =

(4 + n)(3 + u – v) =

(b + c – 2)(5 – x) =

(–s – t – 8)(3 – p) =

(p + 6)(1 – m + n) =

(x² + 2x + 1)(x – 2) = =

(x – 4)(2x² – x – 4) = =

(3a² – a + 5)(2a + 1) = =

(4y + 3)(2y² + 3y – 2) = =

(x² – 3x + 9)(x + 3) = =

(2u – 1)(u² – 4u – 2) = =

(4x² – 5x + 2)(3x – 1) = =

(a² – a + 1)(a + 1) = =

(3u + 2)(u² – 5u – 1) = =

(2x + z)(1 – 2z + z²) = =

(a – b)(2a + b – 1) = =

(u² + v² – 1)(u – v) = =

(x² + x + 1)(x – 1) = =

(m + n)(3m – n – 2) = =

(a² – b)(a + b + 2) = =

(a² – b + 5)(a – b) = =

(a² + ab + b²)(a – b) = =

(a² + 2a + 4)(a – 2) = =

(a – 3)(a² + 3a + 9) = =

(n + 3)(9 – 3n + n²) = =

(4 + x)(x² – 4x + 16) = =

(4 – 2x + x²)(x + 2) = =

(a + b – c)(a – b + c) =

(a – b + c)(–a + b – c) =

(x – y + 2)(x + y – 2) =

(2a – 3b + c)(a + 2b – 3c) =

(3a – 2b – c)(2a + 3b – 3c) =

(2m + n – p)(m + 2n – p) =

(x – xy + y)(xy – x² – 1) =

(a – 2ab + 3b)(2a – ab – 2b) =

(1 – xy + y)(xy – x² – 1) =

(a² – a + 1)(a – a² + 2) =

(y² + 2yz + z²)(y + z) =

(2u + v² + 1)(u + v² – 1) =

2(x + c)(x² + xc + c²) =

3(x – 5)(x² – 3x +2) =

m(m – 1)(m² + 2m + 1) =

b(b² – b – 3)(b + 3) =

5(t – u)(2t² – t + 2) =

–2(b – bc + c)(b – c) =

(a – b)(a + b – ab) + ab(a – b) = =

2a³ + 9 – (a + 1)(a² – a +1) = =

(x – 2)(x + 2) – (x² + 2x + 4)(x – 1) = =

(m – n + 2)(m – 2) + 2(2 – n) = =

(y – 3)² + (y² – y + 3)(y – 3) = =

(a – b)(a² + ab – b²) – (a³ + b³) = =

Если a = –0,5 и b = 5, то значение выражения равно

=

(n – 1)(n² + n – 2) + 3(n + 1) = =

Если n = –3, то значение выражения равно

=

(x – y)(x² – xy + y²) – 2xy(y – x) = =

Если x = 3 и y = –2, то значение выражения равно

=

(x² – x + 1)(x + 2) – x(x – 1) = =

Если x = 0,1, то значение выражения равно

=

(m² + m – 1)(2m – 1) – m²(2m + 1) = =

Если m = –2, то значение выражения равно

=

S_полн =

V =

Подсказка

В случае призмы:
S_полн = 2 · S_осн + S_бок
V = S_осн · H

Sполн =

V =

Подсказка

В случае призмы:
S_полн = 2 · S_осн + S_бок
V = S_осн · H

Lisää aiheesta

Упражнения Б

(a² + 1)(a⁴ – a² + 1) =

(x² – x – 2)(x² + 2) =

(c⁴ – 1)(c³ + c² + 1) =

(ab² – c)(a²b⁴ + ab²c + c²) =

(a + c)(a² – ac + c – a) =

(x – xy)(x² + y² – x + xy) =

(a² + ab + b²)(a² – ab + b²) =

(c³ – c² + 1)(c² + c + 1) =

(a – b)(a³ + a²b + ab² + b³) =

(xⁿ + x²)(xⁿ – x^n–2 + 1) =

(a^m – aⁿ)(a^m+1 + aⁿ⁺¹ + a) =

(2 + bⁿ + b²ⁿ)(bⁿ – 1) =

(x – 1)(x + 1)(x + 1) =

(x + 3)(x + 2)(6x – 3) =

(x – 2)(x – 2)(x + 1) =

(x – 4)(x + 4)(x – 4) =

(a + 2)(a – 2)(a + 3) =

(a + 1)(a + 2)(a + 3) =

(a – 4)(a + 2)(a + 2) =

(a – 5)(a – 4)(a – 3) =

(x + y + z)(x – y – z) + (y + z)² = =

(x + 1)²(x – 1)² – (x² + 1)(x² – x + 1) = =

(a + 3)(a² – 3a + 9) – a(a – 3)(a + 3) = =

(x – 4)(x² – 5x + 3) – (x² – 4x + 3)(x – 5) = =

(c – 1)(c² + 1)(c + 1) + (c² – 1)² = =

(a² – b)(2a² – b – 1) – (–a² + b² + b) = =

Если a = –1 и b = 1, то значение выражения равно

=

(m + n + p)(m² – mn – mp) + m(mn + p²) = =

Если m = 2, $n = \frac{1}{4}$ и p = 3⁰, то значение выражения равно

=

(a + b)³

= (a + b)²(a + b) =

= (a² + 2ab + b²)(a + b) =

= a³ + a²b + 2a²b + 2ab² + ab² + b³ =

= a³ + 3a²b + 3ab² + b³

Объясни все действия.
Возведи в степень, пользуясь полученной формулой.
Ответ представь в виде многочлена стандартного вида. Не пользуйся пробелами. Показатели степени квадрата и куба вводи с помощью кодов Alt+0178 и Alt+0179 или после символа ^, либо копируй отсюда: ², ³.

(c + d)³ =

(a + 2)³ =

(1 + x)³ =

(2m + 1)³ =

Используй полученную формулу.
Записывай без пробелов. Показатели степени квадрата и куба вводи с помощью кодов Alt+0178 и Alt+0179 или после символа ^, либо копируй отсюда: ², ³.

(x – y)³ =

(a – 1)³ =

(1 – b)³ =

(2x – 3y)³ =

(a + b)(a² – ab + b²),

в котором первый множитель – сумма двух одночленов, а второй – неполный квадрат их разности ( в произведении одночленов отсутствует коэффициент 2).

Докажи, пользуясь правилом умножения многочленов, что произведение суммы двух одночленов и неполного квадрата их разности равно сумме кубов этих этих одночленов,

(a + b)(a² – ab + b²) = a³ + b³.