Seni vaadeldud juhuslikud suurused on olnud diskreetsed. See tähendab, et juhusliku suuruse X võimalikke väärtusi on lõplik arv, mis kuuluvad teatud piirkonda ja asuvad üksteisest eraldi.
Järgnevalt vaatleme pidevaid juhuslikke suurusi, mis saavad kõikvõimalikke väärtusi teatud piirkonnast. Järelikult on sellistel suurustel võimalikke väärtusi lõpmatult palju. Seejuures tutvume ühe olulise jaotuse tüübiga, mille abil saab kirjeldada paljusid loodusnähtusi. Selleks on normaaljaotus.
Näide.
Normaaljaotusega on tegemist näiteks vastsündinud tüdrukute ja poiste pikkuse ja kaalu korral. Joonisel 1.35 on 2007. a Eestis sündinud laste jaotus sünnikaalu järgi (rõhtteljel on juhusliku suuruse X väärtused, püstteljel aga vastavad tõenäosused protsentides). Et tegemist on pideva juhusliku suurusega, siis selle üksikuid mõeldavaid väärtusi on lõputult palju ja seetõttu on vastav tõenäosus P(xi) praktiliselt null. Siit järeldub, et mõistlik ei ole näiteks küsida, kui suur on tõenäosus, et lapse sünnikaal on 3276 grammi, vaid tuleb küsida, milline on tõenäosus P(x ≤ 3500) või P(3000 ≤ x ≤ 3500).
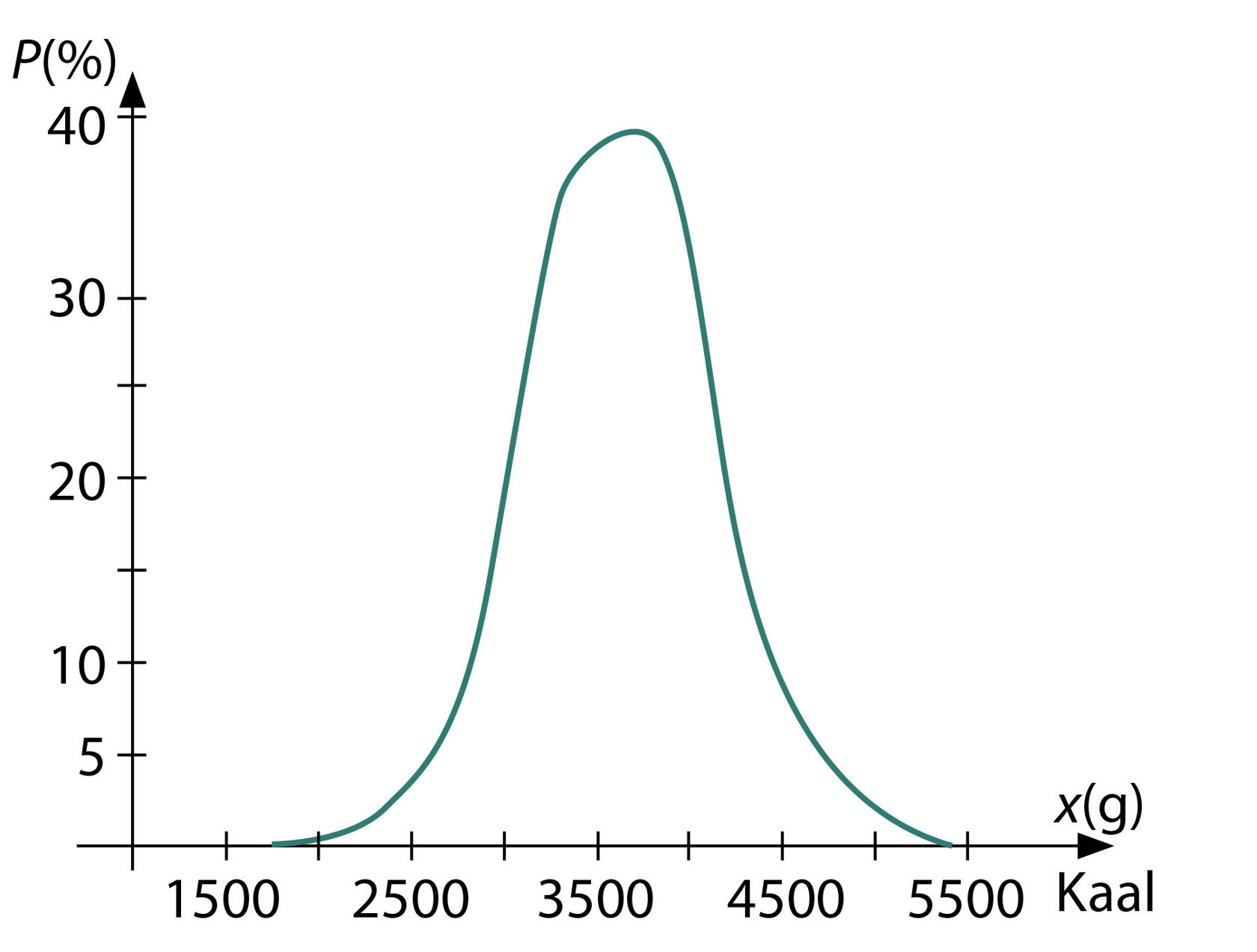 Joon. 1.35 | ||||||
Ideaalne normaaljaotuse graafik on joonisel 1.36, kusjuures –∞ < x < +∞. Graafikut nimetatakse Gaussi kõveraks (Saksa matemaatiku Carl Friedrich Gaussi järgi), ka kella kõveraks.
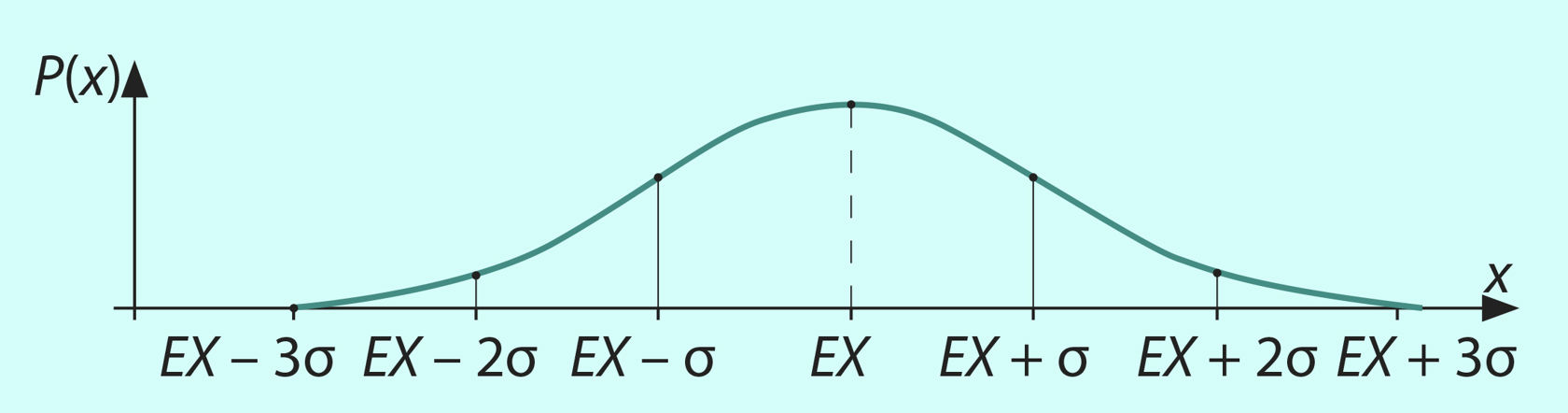 Joon. 1.36 | ||||||
Normaaljaotuse omadusi:
- Normaaljaotus on sümmeetriline oma keskväärtuse suhtes.
- Normaaljaotuse korral ühtivad keskväärtus, mood ja mediaan.
- Kui dispersioon suureneb, muutub graafik madalamaks ja seega ka laiemaks (hajuvus suureneb) ning lamedamaks.
- Gaussi kõvera alune pindala x-teljeni on 1, sest juhusliku suuruse X kõikvõimalike väärtuste tõenäosuste P(X = xi) summa, vaatamata nende tohutule väiksusele, peab olema ikka 1.
- Juhusliku suuruse X väärtustest (vt joon. 1.36) ligikaudu
68% langeb piirkonda [EX – σ; EX + σ],
95% langeb piirkonda [EX – 2σ; EX + 2σ],
99,7% langeb piirkonda [EX – 3σ; EX + 3σ].
Juhusliku suuruse väärtuste selline jaotus on ka üheks tunnuseks, mis viitab normaaljaotusele (nimetatakse ka 3σ-reegliks).
Konkreetsete juhuslike suuruste vaatlemisel, s.t empiiriliste andmete, näiteks laste sünnikaalu korral, saadakse tavaliselt mõnevõrra moonutatud normaaljaotus. Nii on ka joonisel 1.35 esitatud vastsündinud laste kaaluga, vastav graafik ei ole sümmeetriline. Põhjuseks on poiste suurem sünnijuhtude arv ja nende suurem sünnikaal.
Ülesanded A
Ülesanne 225. Mõõtmisvead

Vastus. See jaotus normaaljaotus. Toru läbimõõduks tuleb võtta mm.
Ülesanne 226. Kontrolltöö punktid
Vastus. Kontrolltöö tulemused normaaljaotusele. Kontrolltöö keskmine punktide arv oli .
- Kui suur on tõenäosus, et juhuslikult võetud töö hinne on piirkonnast ?
Vastus. Tõenäosus, et juhuslikult võetud töö hinne on piirkonnast , on .
Ülesanne 227. Suusahüppevõistlus
Vastus. I voorus oli hüpete keskmine pikkus m ja II voorus m. hüppevoor oli ühtlasem. Esimene hüppevoor allub normaaljaotusele, teine hüppevoor allub normaaljaotusele.
