Sündmuse klassikalise tõenäosuse defineerimisel eeldasime, et kõigi võimaluste arv (n) on lõplik. Kuidas aga leida tõenäosust siis, kui kõiki võimalusi vaadeldava sündmuse korral on lõpmatult palju? Tavaliselt on siis ka sündmuse toimumiseks soodsaid võimalusi lõpmatult palju.
Näide 1.
Külma vee toru on 200 m ulatuses maa sees. Torusse tekkis auk. Võimalus augu tekkimiseks on kogu toru ulatuses sama. Kui suur on tõenäosus, et auk on tekkinud maantee all (sündmus A), mille laius on 15 m?
Et toru pikkus on pidev suurus ja augu tekkimise võimalikke kohti (punkte torul) on lõpmatult palju (samuti on soodsaid punkte lõpmatult palju), siis klassikalise tõenäosuse definitsiooni rakendada ei saa. Arutleme piltlikult, tuginedes ettekujutlusele lõplikest suurustest: tundub loomulik, et toru pikkus on võrdeline „punktide arvuga” (lõpmatus!) torul. Kui nii, siis saame ebamäärase mõiste „punktide arv” asendada toru pikkusega ning otsitav tõenäosus peaks olema 15 m : 200 m = 0,075. Nii ta tegelikult ka on, sest geomeetriline tõenäosus defineeritakse lõpliku lõigu L (lõigu all mõtleme ka selle pikkust) korral kui sündmuse jaoks „soodsa pikkuse” l ja kogu pikkuse L jagatis.
Üldiselt defineeritakse geomeetriline tõenäosus järgmiselt:
kui mingi geomeetrilise piirkonna D (lõik, tasandi või ruumi osa), mille mõõde (pikkus, pindala, ruumala) on S, tabamine on kindel, siis selle piirkonna osapiirkonnad, mille mõõde on s, tabamise tõenäosus .
Seejuures eeldatakse, et piirkonna D iga punkti tabamiseks on võrdsed võimalused.
Näide 2.
Kui suur on tõenäosus tabada joonisel 1.13 kujutatud ruudukujulise märklaua värvitud osa?
 Joon. 1.13 | ||||||
Olgu märklaua külg a. Siis värvimata kolmnurkade kaatetid on 0,5a ning nende kolmnurkade pindalade summa on
Värvitud osa pindala on a2 – 0,5a2 = 0,5a2 ja otsitav tõenäosus p = 0,5a2 : a2 = 0,5.
Näide 3.
Poiss viskab palli diameetriga 6 cm läbi ristkülikukujulise ava (joon. 1.14) mõõtmetega 20 × 15 cm. Kui suur on tõenäosus, et pall läbib ava n-ö puhtalt?
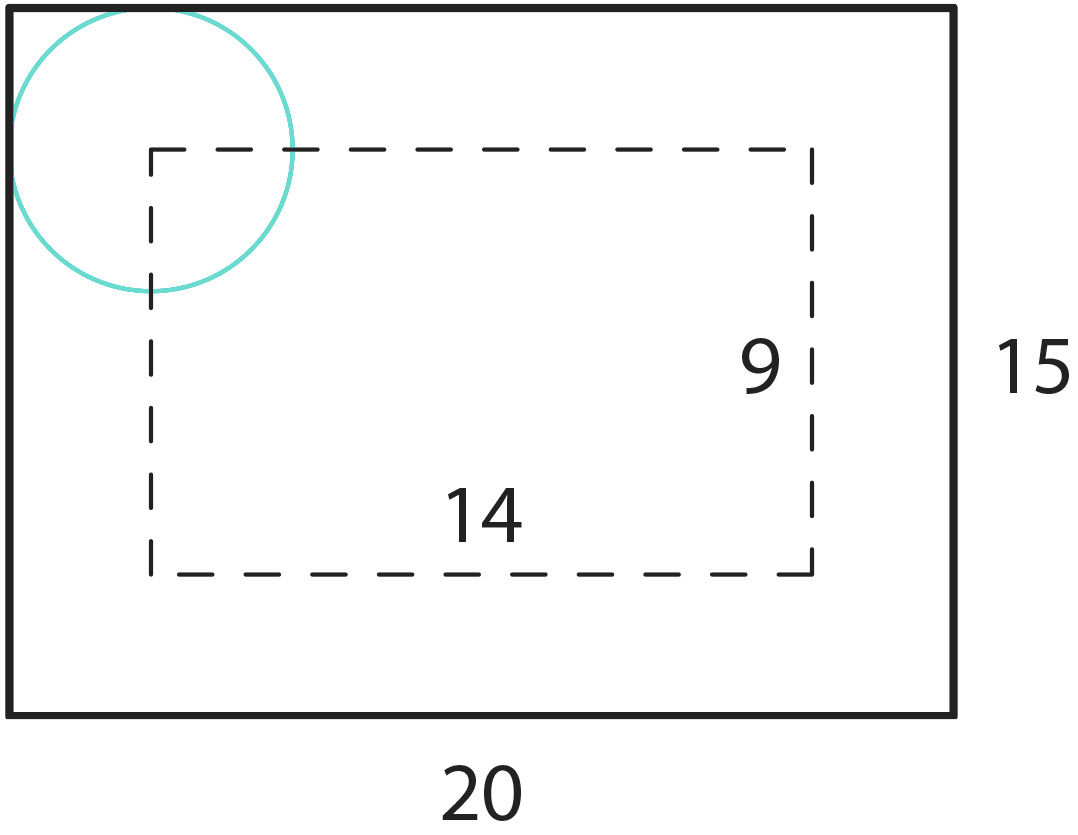 Joon. 1.14 | ||||||
Loeme ava puhtaks läbimiseks ka seda, kui pall puudutab ava serva. Seega, kui palli keskpunkt (joonisel palli suurringi keskpunkt) on katkendliku joonega märgitud ristkülikus, mille mõõtmed on 20 – 6 = 14 cm ja 15 – 6 = 9 cm, siis pall läbib ava. Järelikult
Näide 4.
Iga kahe linnaliinibussi ajaline vahe on 12 minutit. Buss, mis tuleb lõpp-peatusse, seisab seal 3 minutit ja sõidab siis liinile. Bussile mineja jõuab lõpp-peatusse juhuslikul ajal. Kui suur on tõenäosus, et ta jõuab lõpp-peatusse ajal, mil buss seal seisab?
Aja „punktide hulki” 3 min ja 12 min saab kujutada sirgel lõikudena, näiteks 3 cm ja 12 cm. Tuginedes nüüd geomeetrilise tõenäosuse definitsioonile, saame, et p = 3 : 12 = 0,25.
Näide 5.
Maapinna kõrguselt pehkinud lipuvarras (6 m) seisab püsti muruplatsil punktis A (joon. 1.15). Lipuvardast 2 m kaugusel on ringjoone kaare kujuline lillepeenar pikkusega 4 m. Leiame tõenäosuse, et lipuvarras kukub lillepeenrale, kui ta murdub maapinnalt.
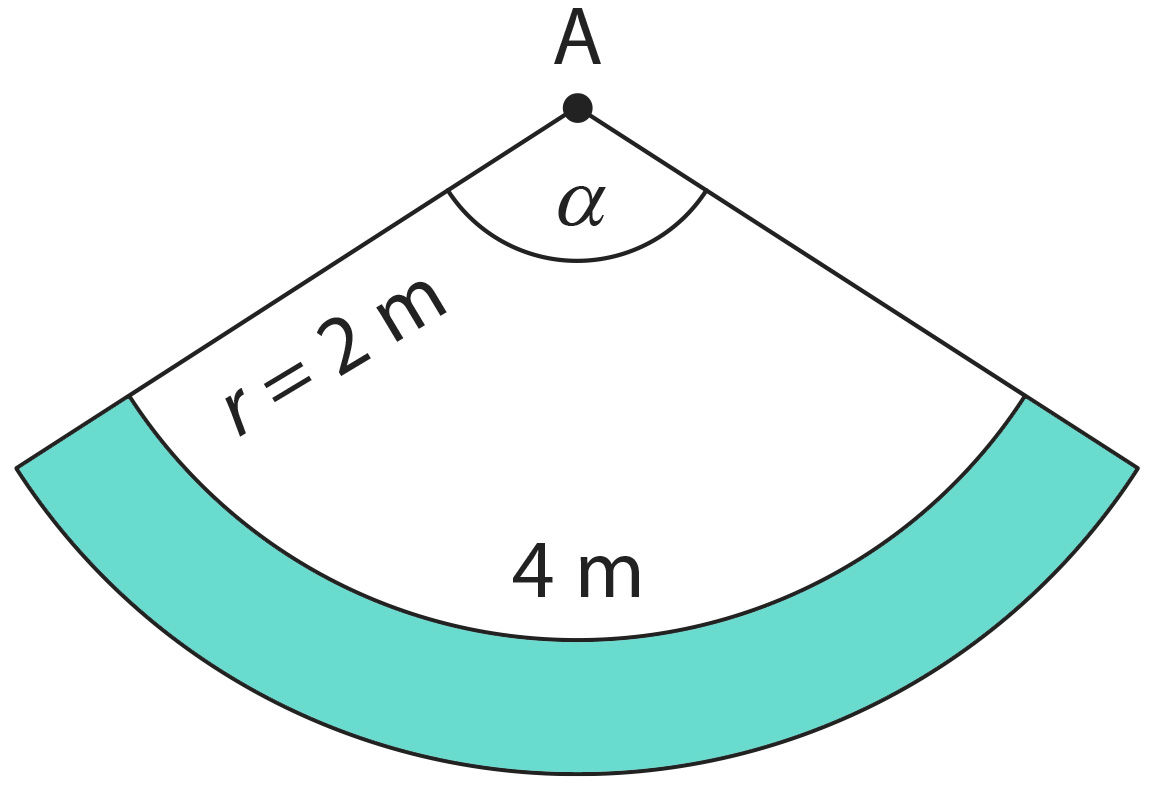 Joon. 1.15 | ||||||
Eeldame, et lipuvarras võib kukkuda võrdse võimalikkusega igas suunas. Kui ta kukub nurka α, on tõenäosuse seisukohalt tegemist soodsa juhuga.
Leiame nurga α. Ringjoone kaare pikkus on 4 m. Seega
Ülesanded A
Ülesanne 130. Märklaua värvitud osa tabamine
 Joon. 1.16 |  | |||||||
p = | p = | |||||||
Ülesanne 131. Valgusfoori tsükkel
Ülesanne 132. Valgusfoori tsükkel
Vastus. Tõenäosus, et juhuslikul ajamomendil foori juurde jõudes pääsete kohe edasi, on siis
Ülesanne 133. Valgusfooride tsüklid
Vastus. Tõenäosus, et jalakäija saab juhuslikul ajamomendil fooride juurde jõudes edasi peatumata, on siis
Ülesanne 134. Mündi viskamine lauale
Vastus. Tõenäosus, et lauale visatud eurone metallraha ei lõiku joontega, on
Ülesanne 135. Mündi viskamine lauale
Vastus. Tõenäosus, et lauale visatud üheeurone münt ei lõiku joontega, on
Ülesanne 136. Puu langemine
Vastus. Tõenäosus selleks on
Ülesanded B
Ülesanne 137. Märklaua värvitud osa tabamine
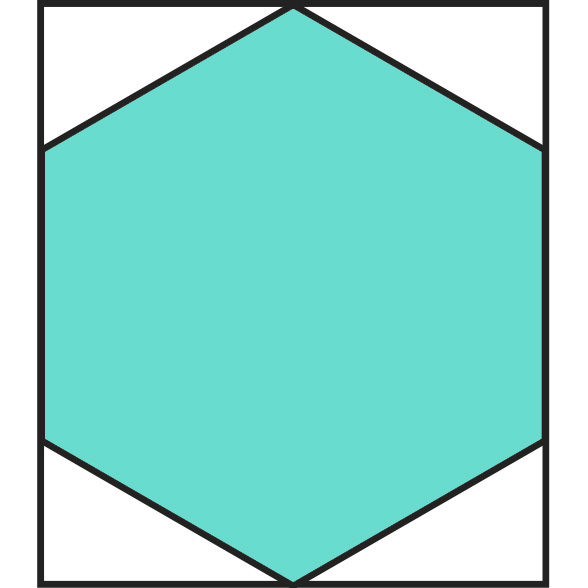 |  | |||||||
p = | p = | |||||||
Ülesanne 138. Kiviga aknasse viskamine
Vastus. Aknakese purunemise tõenäosus on
Ülesanne 139. Tartu raekoja platsil purskkaevu juures kohtumine
Vastus. Tõenäosus, et Oskar ja Saara kohtusid, on
