Juhusliku suuruse karakteristikud

Juhusliku suuruse X jaotust, mis on esitatud tabeliga

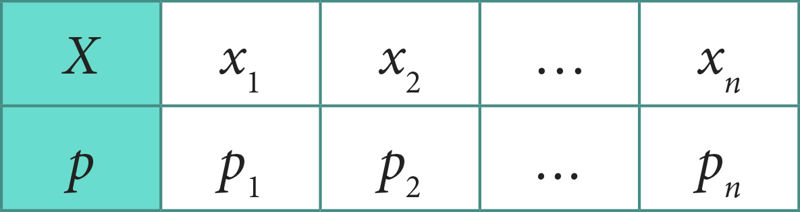ise­loomustatakse mitmete arv­karakteristikutega (nagu statistilise kogumi tunnuse sagedus­tabeli või jaotus­tabeli korral). Need on juhusliku suuruse väärtuste paiknemist arv­teljel ise­loomustav keskmine väärtus, mida nimetatakse kesk­väärtuseks ja väärtuste hajuvust ise­loomustavad näitajad dispersioon ning standard­hälve.

Juhusliku suuruse X kesk­väärtuseks nimetatakse arvu

EX = p1x1 + p2x2 + … + pnxn.

Näide 1.

Täringu viskamisel tuleva silmade arvu jaotus on tabelis.

Täringu viskamisel tuleva silmade arvu X kesk­väärtus on

EX=\frac{1}{6}\cdot1+\frac{1}{6}\cdot2+\frac{1}{6}\cdot3+\frac{1}{6}\cdot4+\frac{1}{6}\cdot5+\frac{1}{6}\cdot6 = 21 : 6 = 3,5.

See tähendab, et täringu korduval viskamisel tuleb ühe viskega keskmiselt 3,5 silma, järelikult kümne viskega keskmiselt 35 silma.

Juhusliku suuruse X dispersiooniks nimetatakse kesk­väärtuse suhtes arvutatud hälvete ruutude kesk­väärtust DX = E(X – EX)2.

Seega

DX = p1(x1 – EX)2 + p2(x2 – EX)2 + … + pn(xn – EX)2.

Näide 2.

Täringu korduval viskamisel tuleva silmade arvu X dispersioon

DX=\frac{1}{6}\cdot\left(1-3,5\right)^2+\frac{1}{6}\cdot\left(2-3,5\right)^2+\frac{1}{6}\cdot\left(3-3,5\right)^2+\frac{1}{6}\cdot\left(4-3,5\right)^2+\frac{1}{6}\cdot\left(5-3,5\right)^2+\frac{1}{6}\cdot\left(6-3,5\right)^2 = 17,5 : 6 ≈ 2,917.

Juhusliku suuruse X standard­hälbeks nimetatakse ruut­juurt dispersioonist,

σ=DX.

Näide 3.

Täringu viskamisel (näide 2) tuleva silmade arvu X standard­hälve

σ = \sqrt{DX} = \sqrt{2,917} ≈ 1,708.

Tuletame dispersiooni arvutamiseks ka teist­suguse valemi. Et kesk­väärtus EX = p1x1 + p2x2 + … + pnxn, siis avaldis p1x12 + p2x22 + … + pnxn2 annab juhusliku suuruse X2 kesk­väärtuse EX2. Nüüd

DX = p1(x1 – EX)2 + p2(x2 – EX)2 + ... + pn(xn – EX)2 = p_1\left(x_1^2-2x_1EX+\left(EX\right)^2\right)+p_2\left(x_2^2-2x_2EX+\left(EX\right)^2\right)+...+p_n\left(x_n^2-2x_nEX+\left(EX\right)^2\right) = p_1x_1^2+p_2x_2^2+...+p_nx_n^2-2EX\left(p_1x_1+p_2x_2+...+p_nx_n\right)+\left(EX\right)^2\left(p_1+p_2+...+p_n\right) = EX^2-2\cdot EX\cdot EX+\left(EX\right)^2 = EX^2-\left(EX\right)^2.

Seega

DX = EX2 – (EX)2

ja

σ=EX2-(EX)2.

More like this
More options

Ülesanded A

Ülesanne 202. Kahe täringu korraga viskamine

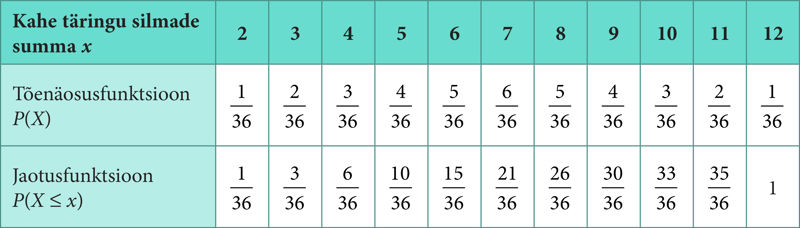
Vastus. EX = ; σ = .

Ülesanne 203. Kahe­teist­tahuline täring

Vastus. EX = ; σ = .

Ülesanne 204. Loterii

Vastus. Keskmine võidu suurus ühe loterii­piletiga oli  € ja standard­hälve oli . Loterii töötas , mille suurus oli  eurot.

Ülesanne 205. Raha jagamine

Vastus. Mõlema poisi keskmine võidu­summa on ja standard­hälve on .

More like this
More options