Naturaalarvud, järguühikud, järgud
Viiendasse klassi tuleb uus matemaatikaõpetaja Kaarel Kümme. Esimeses tunnis jutustatakse, mida keegi suvepuhkuse ajal on teinud. Mõnelgi õpilasel on ka matemaatikat vaja läinud kas poes sisseoste tehes, matkaradadel olles või mujal oma teenitud raha kasutamisel.
Jutusta sinagi oma suvistest tegemistest.
Muidugi on suvel mõndagi ka ununenud. Seepärast meenutame kõigepealt olulisemat. Arvud
0, 1, 2, 3, ..., 9, 10, 11, ..., 100, 101, ..., 999, 1000, 1001, ...
on naturaalarvud[mõiste: Naturaalarv – üks arvudest 0, 1, 2, 3, ...]. Neist arvud
1, 10, 100, 1000, ...
on järguühikud[mõiste: Järguühikud – arvud 1, 10, 100, 1000 jne. Need arvud on loendamisel ühikuteks (üheline, kümneline, sajaline, tuhandeline jne).]. Naturaalarvud kirjutatakse numbrite
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
abil.
Arvu kirjutis koosneb järkudest. Lugemise kergendamiseks jaotatakse järgud kolme kaupa klassidesse[mõiste: Klass – suuremate naturaalarvude lugemiseks ja kirjutamiseks jaotatakse nende järgud alates paremalt kolmekaupa rühmadesse. Neid rühmi nimetatakse klassideks. Kui arvus on enam kui neli järku, siis jäetakse klasside vahele suurem vahe.], alates paremalt. Näiteks
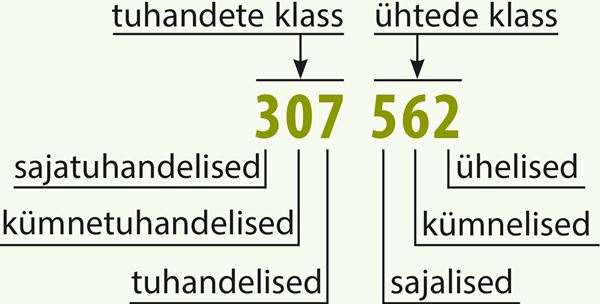
Pane tähele!
Eesti keeles kirjutame sajad kokku (nt seitsesada), aga tuhanded lahku (seitse tuhat).
Kirjutatud arvu loetakse: kolmsada seitse tuhat viissada kuuskümmend kaks. Iga number näitab, mitu vastava järgu ühikut sellesse arvu kuulub. Iga järgu 10 ühikut moodustavad uue, kõrgema järgu ühiku. Seepärast nimetatakse seda arvude kirjutamise viisi kümnendsüsteemiks[mõiste: Kümnendsüsteem – positsiooniline arvusüsteem, milles iga numbri tähendus oleneb tema asukohast (positsioonist) arvus. Liikudes paremalt vasakule tähistab iga number eelmisest 10 korda suuremaid ühikuid.].
Kui arvus on enam kui neli numbrit (järku), siis jäetakse klasside vahele suurem vahe.
1. Naturaalarvud, järguühikud, järgud
Loe arve. Nimeta iga arvu klassid ja kõik järgud ning ütle, mitu ühikut on igas järgus.
24 506, 1378, 109 267, 346, 200 501, 30 330, 20 021, 900 280
Arvu esitamine järkarvude summana
Iga naturaalarvu, milles on enam kui üks number, saab esitada järkarvude[mõiste: Järkarv – arv, mis kirjutatakse ainult ühe nullist erineva numbri ja sellele järgnevate nullide abil.] summana. Näiteks
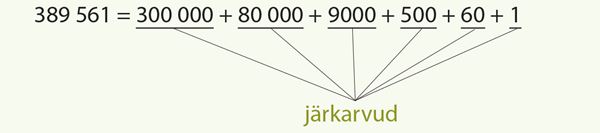
Järkarvus on ainult üks nullist erinev number.
Ülesanded A
 | ||||||||
0; 5; 10; 15; 3; 8; 4; 20; 50; 30
Liida:
Lahuta (mis võimalik):
Korruta:
Jaga (mis ilma jäägita võimalik):
Jäägita jagamisi on võimalik tk.
Vastus. Need kauplused müüsid selles kuus kaupa kokku € eest.
Nende andmete järgi saaks veel arvutada
Vastus. Hr Kuusk sai selles kuus € rohkem palka, sest .
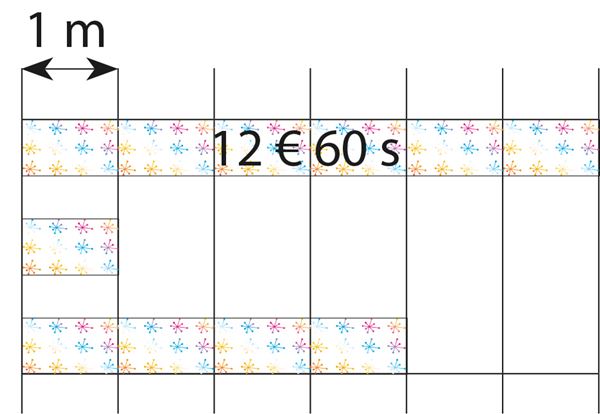
Vastus. 1 meeter seda riiet maksab € s ja 4 meetrit seda riiet maksab € s.
8 seemet – saagiks saadi 8 korda rohkem kartuleid, kui maha pandi.
Vastus. Saadi kg kartuleid ja selle autoga tuleks teha reisi.
Vastus. Aias on õunapuud.

Vastus. sest vaja läks kasti.
Vastus. Laoplatsil on palki.
Vastus. Rong läbis 4 tunniga km, 5 tunniga km ja 7 tunniga km.
Vastus. Reisija kulutab lennukiga lennates korda vähem aega.
 aknaraami pikkus – ristküliku ümbermõõt klaasipind – ristküliku pindala | ||||||||
Ülesanded B
 |
||||||||
Pane tähele!
Tavakeeles ei kasutata sõna number nii rangelt kui matemaatikas.
 |
||||||||
 |
||||||||
1) sada kümnelist? | 100 · = |
2) sada kümnetuhandelist? | · = |
3) tuhat sajalist? | · = |
Suurim kahekohaline arv on .
Vastus. Suurima kahekohalise arvu naaberarvud on ja .
Vähim neljakohaline arv on .
Vastus. Vähima neljakohalise arvu naaberarvud on ja .
Vastus. See arv on .
Suurim kolmekohaline arv on ja vähim kolmekohaline arv on .
Vastus. Nende arvude summa on ja vahe on .
Suurim kolmekohaline arv on ja suurim ühekohaline arv on .
Vastus. Nende arvude korrutis on ja jagatis on .
Vastus. Nende arvude summa on .
Vastus. Kuus aastat tagasi oli ema pojast korda vanem.
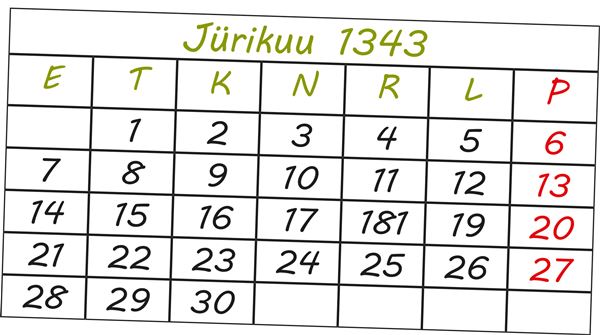 | ||||||
Vastus. Käesoleval aastal oli . Jüriöö ülestõusu aastapäev.
Esimesel päeval luges Gea lehekülge, teisel päeval lehekülge ja kolmandal päeval lehekülge.
Kokku luges ta kolme päevaga lehekülge.
Vastus.
 |
||||||
Vastus. Sellest kangast saaks õmmelda täiskasvanute jopet.
Vastus. Maire kavatses joosta igal hommikul m.
Vastus. Värviti dm2 pinda.
Vastus. Istutada tuleb lilletaime.
Vastus. Valiti arv .
