Eksponent­funktsioon y = ex

Mitmete elu­nähtuste kirjeldamisel esineb eksponent­funktsioon, mille aluseks on arv e (≈ 2,72) või selle pöörd­väärtus e–1. Funktsioonidel y = ex (graafik joonisel 3.11) ja y = (e–1)x ehk y = e–x (graafik joonisel 3.12) on samad omadused, mis funktsioonil y = ax, kui a > 1 ja 0 < a < 1.

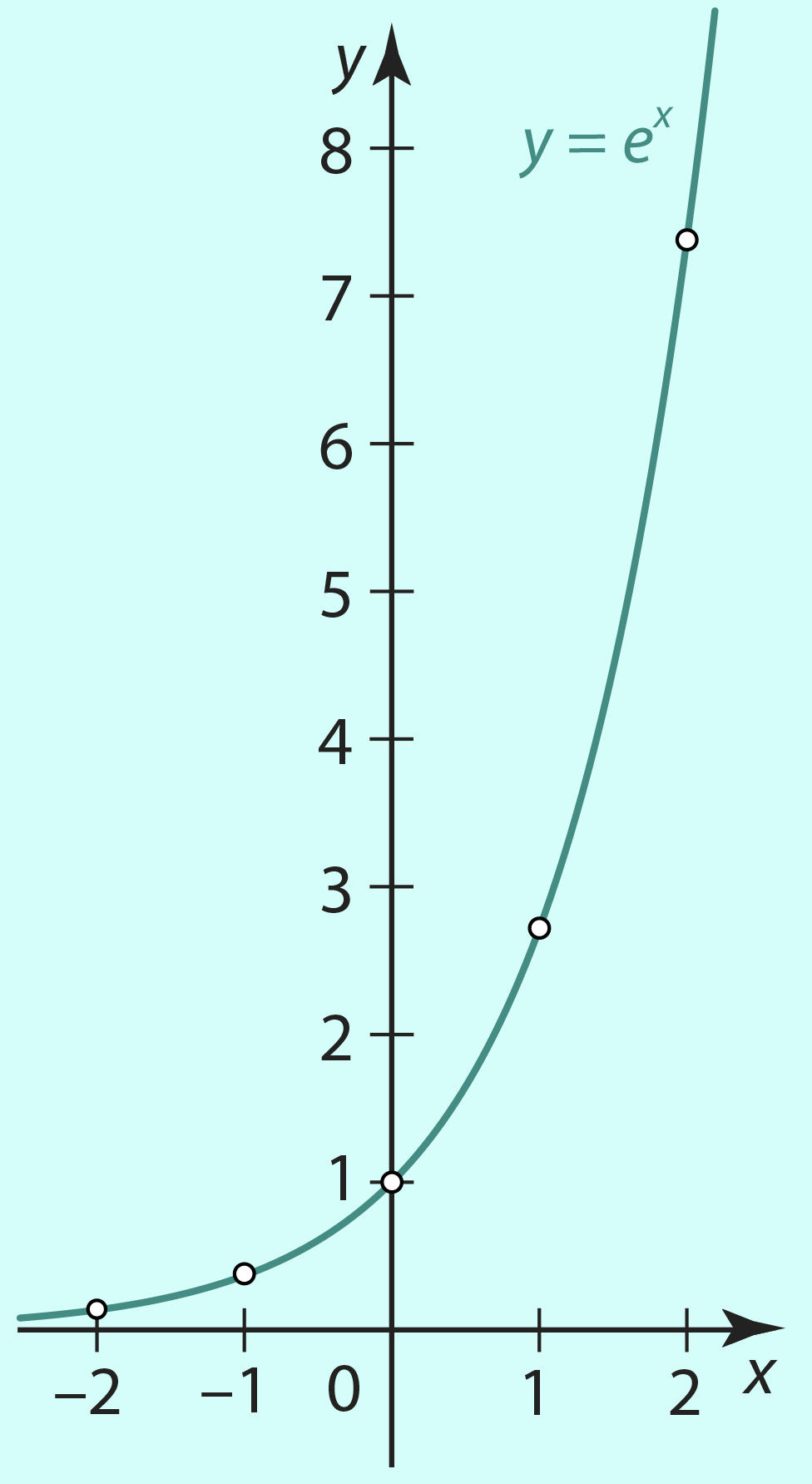Joon. 3.11
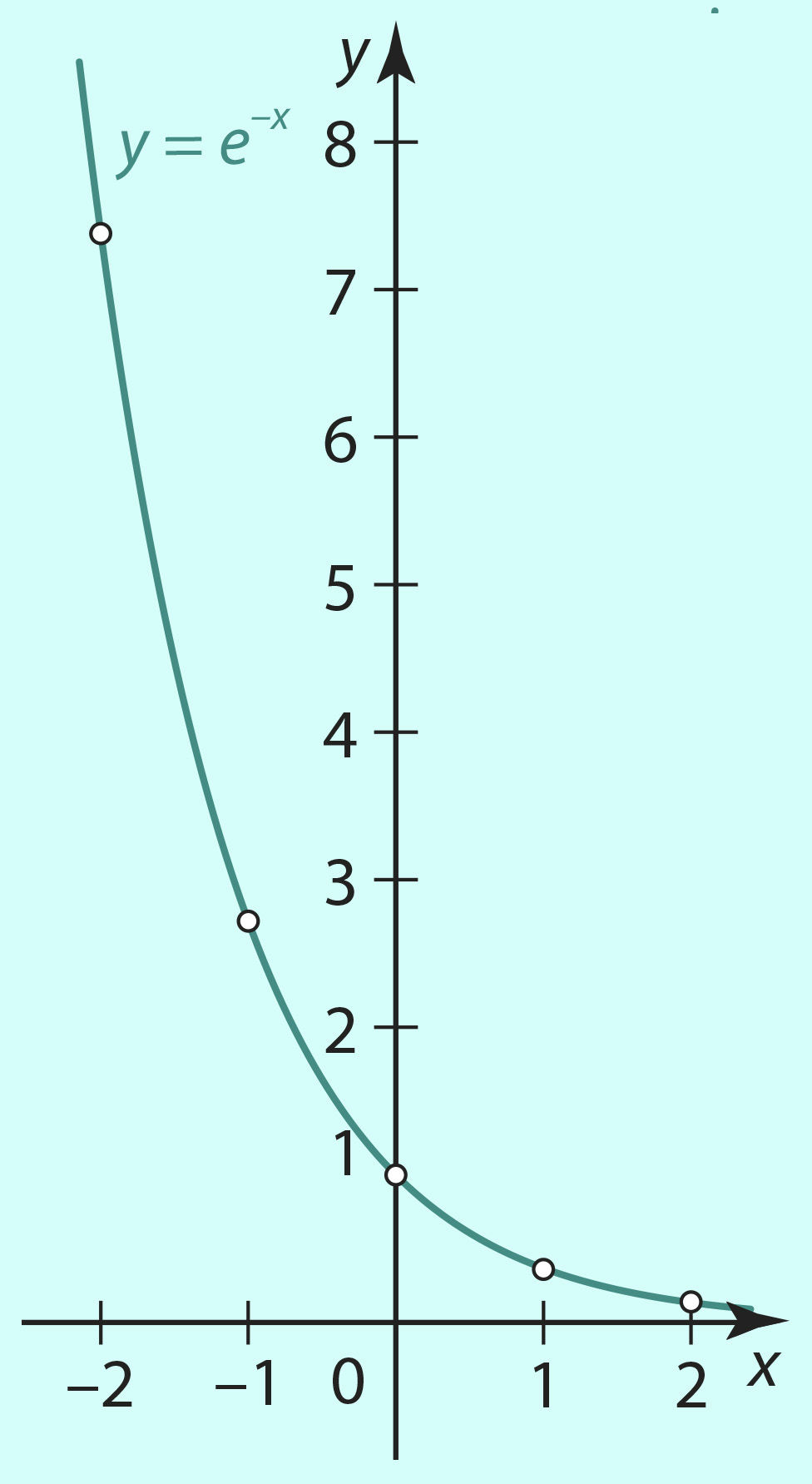Joon. 3.11

Funktsioonide y = ex ja y = e–x väärtusi saab leida vastavatest tabelitest või tasku­arvutiga, millel on klahv ex. Selle kasutamine on analoogiline klahvi 10x kasutamisega.

Näide 1.

Aste e4,014 arvutatakse olenevalt arvutist skeemi 4,014 ex või ex 4,014 = kohaselt; e4,014 ≈ 55,3679.

Skeemi 0,0001 +/– ex või vastavalt ex 0,0001 +/– = järgi arvutades saadakse, et e–0,0001 ≈ 0,9999000.

Kui tasku­arvutil on klahvi +/– asemel klahv (–), tuleb tavaliselt märk “–” sisestada enne arvu.

Näide 2.

Summa e2,5 + e–0,201 arvutatakse olenevalt arvutist skeemi 2,5 ex + 0,201 +/– ex = või ex 2,5 + ex 0,201 +/– = järgi. Tulemuseks saame, et e2,5 + e–0,201 ≈ 13,0004.

Näite 2 ees­kujul saab arvutada e^{x_1}-e^{x_2}, e^{x_1}\cdot e^{x_2} ja e^{x_1}:\ e^{x_2}. Kahel viimasel juhul võib tulemuse leida ka avaldiste e^{x_1+x_2}  ja e^{x_1-x_2} järgi.

Näide 3.

Astme e^{3,2-\sqrt{3}} arvutame skeemi ( 3,2 – √ 3 ) = ex või ex ( 3,2 – √ 3 ) = järgi. Tulemuseks saame, et e^{3,2-\sqrt{3}}\approx4,3403.

Näide 4.

Hindame, kumb on suurem, kas e–3 või e–5. Arvutuslikult on selleks ots­tarbekas leida nende jagatis. Kui see tuleb ühest suurem, on jagatav suurem jagajast, kui see tuleb alla ühe, on vastu­pidi, ja ühe korral on jagatav ning jagaja võrdsed. Et e–3 : e–5 = e–3 – (–5) = e2 > 1, siis e–3 > e–5.

Ka funktsiooni y = ex graafikult saame tulemuse lihtsalt. Et funktsioon on kasvav, siis suuremale argumendi väärtusele (–3 > –5) vastab ka suurem funktsiooni väärtus, mis­tõttu e–3 > e–5.

More like this
More options

Ülesanded A

Ülesanne 607. Arv e

e^2 = 

e^{5,03} = 

e^{0,45} = 

e^{1,258} = 

e^{-3} = 

e^{-1,3} = 

e^{-0,08} = 

e^{-9} = 

\sqrt[3]{e} = 

\sqrt{e} = 

\sqrt[7]{e} = 

\sqrt[4]{e} = 

\sqrt{e^3} = 

\sqrt[5]{e^2} = 

\sqrt[4]{e^{-3}} = 

\sqrt[7]{e^{4,04}} = 

Ülesanne 608. Arv e

e^{0,76\cdot1,7-2,56} = 

e^{55\cdot0,083+14,72} = 

0,264\cdot\sqrt[3]{e}+5,606 = 

Ülesanne 609. Arv e

e^5\cdot e^2 = 

e^{4,3}:\ e^{-1,7} = 

\left(e^{0,85}\right)^2 = 

e^{\sqrt{3}}\cdot e^{-2\sqrt{3}} = 

e^{2+\sqrt{5}}:\ e^{1+\sqrt{5}} = 

\left(e^{\sqrt{6}}\right)^{2\sqrt{6}} = 

2^e\cdot5^e = 

7^{2e}:\ 7^{3e} = 

Ülesanne 610. Eksponent­funktsiooni graafik

610.1 Eksponent­funktsiooni graafik

Konstrueerige funktsiooni graafik.

y=2e^x

610.2 Eksponent­funktsiooni graafik

Konstrueerige funktsiooni graafik.

y=0,6e^x

610.3 Eksponent­funktsiooni graafik

Konstrueerige funktsiooni graafik.

y=e^{x-2}

610.4 Eksponent­funktsiooni graafik

Konstrueerige funktsiooni graafik.

y=2,5e^{-x}

Ülesanne 611. Võrdlemine

e^3  e^5

e^{0,2}  e^{0,4}

e^8  e^{-0,08}

e^{-3}  e^{-2}

Ülesanne 612. Eksponent­võrrandi lahendamine

e^{2x}=e^8
x = 

e^{3x-1}=1
x = 

e^{4-3x}=e^7
x = 

e^{-x}=e^3
x = 

e^{2x-2}=0
x = 

e^{2x+3}=e^{2+2x}
x = 

Ülesanne 613. Õhu­rõhk

Vastus. 2000 m kõrgusel mere­pinnast on õhu­rõhk  mmHg ja 4000 m kõrgusel  mmHg.

More like this
More options

Ülesanded B

Ülesanne 614. Eksponent­võrratuse lahendamine

e^x<e^8
x  

e^x>1
x  

e^x>e
x  

e^x<e^{0,66}
x  

e^{-x}>e^{-4}
x  

e^{-x}<e^{-1,1}
x  

2e^x>e^x
x  

e^x<5^x
x  

e^{-x}<4^x
x  

Ülesanne 615. Ahel­joon

Leidke funktsiooni y=\frac{e^x+e^{-x}}{2} määramis­piirkond, null­kohad, positiivsus­piirkond ja negatiivsus­piirkond. Konstrueerige, näiteks arvuti abil, funktsiooni graafik vahemikus –3,5 < x < 3,5. Saadud joont nimetatakse ahel­jooneks, sest selle joone kuju võtab raske ahel, mis on kinnitatud kahest otsast (samuti raske kaela­kee). Milline on selle funktsiooni muutumis­piirkond, kasvamis- ja kahanemis­vahemik?

Vastus. X = ; X_0 = ; X^+ = ; X^- = ; Y = ; X\uparrow = ; X\downarrow = .

Ülesanne 616. Ahel­joon

Et näha ahel­joone ja parabooli erinevusi, konstrueerige ühte ja samasse koordinaat­teljestikku funktsioonide y=\frac{e^x+e^{-x}}{2} ja y = x2 + 1 graafikud. Milliseid erinevusi märkate? Kumb graafikutest ja millises piir­konnas tõuseb (langeb) järsemalt?

Ülesanne 617. Pliiga saastatus

Tee­äärse maa­pinna saastamist pliiga (milli­grammi ruut­meetri kohta aastas) arvutatakse valemist C=0,012\cdot A\cdot e^{-0,11k}+0,37\sqrt[3]{A}, kus A on liiklus­tihedus (liiklus­vahendite arv) öö­päevas ja k on kaugus meetrites tee­servast. Konstrueerige suuruste C ja k vahelise sõltuvuse graafikud teede kohta, kus liikus öö­päevas 1000 liiklus­vahendit ja kus 3000 liiklus­vahendit (Eestis oli selliseid teid 1980-ndatel aastatel umbes 2200 km). Lugege ohutu saastatuse piiriks 10 mg/m2 pliid aastas. Mitme­kordselt ületas kummalgi juhul saastatus lubatud normi tee­peenral? Kui kaugel tee servast algas ohutu piir­kond kummagi liiklus­tiheduse korral?

Vastus. 1000 liiklus­vahendi korral ületas saastatus tee­peenral lubatud normi  korda ja 3000 liiklus­vahendi korral  korda. Ohutu piir­kond tee servast algas 1000 liiklus­vahendi korral umbes  m kaugusel ja 3000 liiklus­vahendi korral umbes  m kaugusel.

Ülesanne 618. Pliiga saastatus

Tee­äärse maa­pinna saastamist pliiga (milli­grammi ruut­meetri kohta aastas) arvutatakse valemist C=0,012\cdot A\cdot e^{-0,11k}+0,37\sqrt[3]{A}, kus A on liiklus­tihedus (liiklus­vahendite arv) öö­päevas ja k on kaugus meetrites tee­servast.

  • Konstrueerige suuruste A ja C vahelise sõltuvuse graafikud, kui
    1. k = 0 m ja
    2. k = 10 m.
  • Millise liiklus­tiheduse korral ületas saastatus lubatud piiri 10 mg/m2 tee­peenral ja teest 10 meetri kaugusel? Andke vastus 100 auto täpsusega.
    Vastus. Tee­peenral ületas saastatus lubatud piiri liiklus­tiheduse  autot öö­päevas korral ja 10 meetri kaugusel liiklus­tiheduse  autot öö­päevas korral.
  • Kui öö­päevas läbis teed üle 3000 auto, soovitati jätta tee äärde 20 m laiune puhver­tsoon, kus ei kasvatataks põllu­kultuure. Kontrollige arvutuslikul teel, kas sellise laiusega puhver­tsoonist piisab.
Ülesanne 619. Eksponent­funktsiooni graafik

Joonestage koordinaat­teljestikku funktsiooni y = ex graafik. Konstrueerige sellesse teljestikku ka funktsioonide 1) y = ex + 2, 2) y = ex – 3, 3) y = 2 · ex graafikud.

More like this
More options