Geomeetriline jada

Ülesanne 324. Jada üldliige

1; 2; 4; 8; 16; ; ; …

2; 1; \frac{1}{2}; \frac{1}{4}; \frac{1}{8}; ; ; …

–3; –3²; –3³; –3⁴; –3⁵; ; ; …

–3; 6; –12; 24; –48; ; ; …

Leidke seaduspärasus ja jätkake antud jadasid kahe liikme võrra.
Mida ühist märkate nendes jadades?
Leidke jada üldliige.

1; 2; 4; 8; 16; …	a_n =
2; 1; \frac{1}{2}; \frac{1}{4}; \frac{1}{8}; …	a_n =
–3; –3²; –3³; –3⁴; –3⁵; …	a_n =
–3; 6; –12; 24; –48; …	a_n =

Jada, milles teisest liikmest alates on iga liikme ja sellele eelneva liikme jagatis konstantne, nimetatakse geomeetriliseks jadaks.

Kui jada (a_n) on , siis on jagatis \frac{a_n}{a_{n-1}} ühesugune iga n > 1 korral. Seda jagatist nimetatakse geomeetrilise jada teguriks ja tähistatakse tähega q. Seega \frac{a_n}{a_{n-1}}=q ehk a_n=a_{n-1}q.Kui näiteks geomeetrilises jadas a₁ = 6 ja q = 2, saame jada 6; 12; 24; 48; … . Kui a₁ = 3 ja q = 1, saame konstantse jada 3; 3; 3; … .

Ülesanne 325. Geomeetriline ja aritmeetiline jada

$\frac{1}{3}$ ; $\frac{- 1}{6}$ ; $\frac{1}{12}$ ; $\frac{- 1}{24}$ ; ...
$0,2$ ; $0,6$ ; $1,8$ ; $5,4$ ; …
$\sqrt{7}$ ; $7$ ; $7 \sqrt{7}$ ; $49$ ; ...
$\frac{1}{3}$ ; $\frac{1}{6}$ ; $- \frac{2}{3}$ ; $- 1 \frac{1}{6}$ ; ...
$\frac{1}{2}$ ; $\frac{1}{3}$ ; $\frac{1}{4}$ ; $\frac{1}{5}$ ; ...
$1$ ; $3$ ; $9$ ; $27$ ; …
$- 24$ ; $- 16$ ; $- 8$ ; $0$ ; …
$1$ ; $2$ ; $3$ ; $4$ ; …
$- 8$ ; $- 8$ ; $- 8$ ; $- 8$ ; …
$- 16$ ; $- 8$ ; $- 4$ ; $- 2$ ; …

Ülesanne 326. Geomeetrilise jada tegur

Geomeetriline jada	Jada tegur
1; 3; 9; 27; …	q =
\frac{1}{3};\ \frac{-1}{6};\ \frac{1}{12};\ \frac{-1}{24};\ \dots	q =
\sqrt{7};\ 7;\ 7\sqrt{7};\ 49;\ \dots	q =
0,2; 0,6; 1,8; 5,4; …	q =
–16; –8; –4; –2; …	q =
–8; –8; –8; –8; …	q =

Joonestage iga jada jaoks arvtelg ja kandke sellele jada 6 esimest liiget.
Uurige jada sõltuvalt teguri q märgist (vaadelge eraldi jadasid, kus q > 0 ja q < 0). Milliseid järeldusi teete? Kontrollige oma väiteid veel mõne jada korral.

Missuguseid väärtusi ei tohi geomeetrilise jada teguril olla? Miks?
Missuguseid väärtusi ei tohi geomeetrilise jada liikmetel olla? Miks?

Еще на эту тему

Geomeetrilise jada üldliige

Kui on teada geomeetrilise jada (a_n) esimene liige a₁ ja q, on võimalik leida selle jada mis tahes liiget:a₂ = a₁q, a₃ = a₂q = a₁qq = a₁q², a₄ = a₃q = a₁q²q = a₁q³ehk üldiselt a_n = a₁q^n–1.

Geomeetrilise jada (a_n) üldliige avaldub kujul a_n = a₁q^n–1.

Näide 1. Geomeetrilises jadas on antud a₅ = 16 ja a₁ = 81. Leiame jada teguri q.Et a_n = a₁q^n–1, siis a₅ = a₁q⁴. Seega 16 = 81q⁴, millest q^4=\frac{16}{81} ning q=\pm\sqrt[4]{\frac{16}{81}}=\pm\frac{2}{3}. Järelikult leidub kaks sellist geomeetrilist jada:

81; –54; 36; –24; 16; …; 81\cdot\left(-\frac{2}{3}\right)^{n-1}; …
81; 54; 36; 24; 16; …; 81\cdot\left(\frac{2}{3}\right)^{n-1}; ...

Näide 2. Üks koolerapisik jaotub iga poole tunni järel kaheks pisikuks. Kui palju koolerapisikuid on tekkinud ühest koolerapisikust 5 tunni möödudes?

Kui algul on üks koolerapisik, siis poole tunni pärast on kaks pisikut, sealt edasi poole tunni pärast 4 pisikut jne (joonis 2.6). Tekib geomeetriline jada, kus a₁ = 1, q = 2. Et a₁ on pisikute arv vaatluse algul, siis tuleb meil leida a₁₁:a_{11}=a_1q^{10}=1\cdot2^{10}=1024.

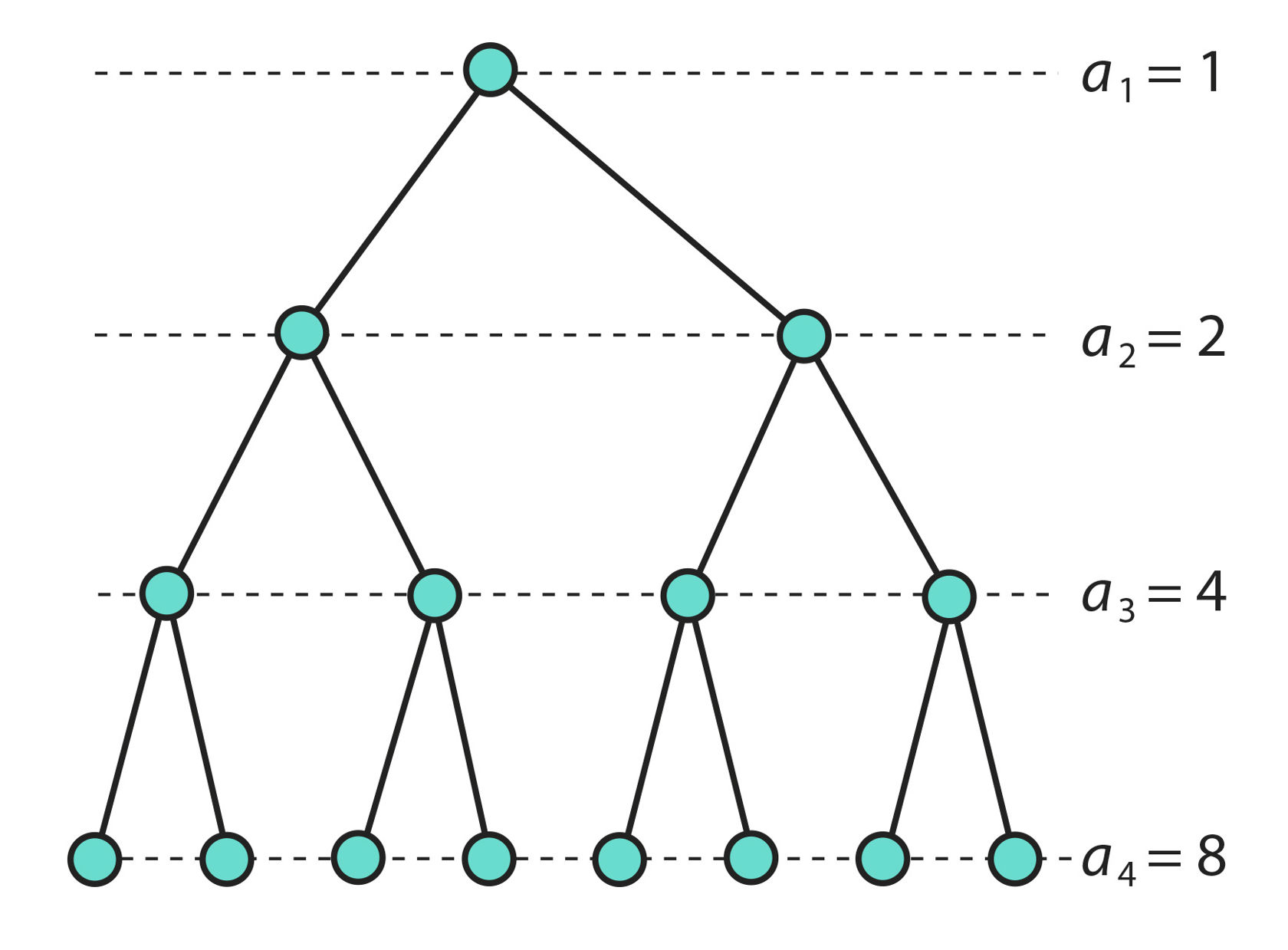Joon. 2.6

Vastus. Viie tunni pärast on 1024 pisikut.

Еще на эту тему

Ülesanded A

Ülesanne 327. Geomeetriline jada

a₁ = 1, q = 2

Vastus. a_n = , a₆ = .

a₁ = 2, q = –3

Vastus. a_n = , a₆ = .

a₁ = 0,125, q = –4

Vastus. a_n = , a₆ = .

a₁ = –10, q = 0,5

Vastus. a_n = , a₆ = .

a_1=-\frac{5}{6}, q=-\frac{3}{5}

Vastus. a_n = , a₆ = .

a₁ = 51, q = 10^–1

Vastus. a_n = , a₆ = .

a_1=\sqrt{2}+\sqrt{3}, q=\sqrt{6}

Vastus. a_n = , a₆ = .

a_1=-256, q=\frac{1}{4}

Vastus. a_n = , a₆ = .

Ülesanne 328. Geomeetriline jada

q = 5, a₃ = 125

Vastus. a₁ =

q = –0,2, a₅ = 12

Vastus. a₁ =

q = –1, a₂₀ = 7

Vastus. a₁ =

q = 2, a₈ = 720

Vastus. a₁ =

q=\sqrt{3}, a₅ = 24

Vastus. a₁ =

q=-\sqrt{5}, a_6=75\sqrt{5}

Vastus. a₁ =

Ülesanne 329. Geomeetriline jada

a₂ = 6, a₄ = 24

Vastus. a₉ = või a₉ =

a₃ = –9, a₅ = –81

Vastus. a₉ =

a₅ = 2, a_{10}=\frac{1}{16}

Vastus. a₉ =

a_5=\frac{1}{40}, a_8=\frac{1}{40000}

Vastus. a₉ =

Ülesanne 330. Geomeetriline jada

Vastus. Need arvud on ja .

Ülesanne 331. Geomeetriline jada

Vastus. Need arvud on , ja .

Ülesanne 332. Õhurõhk

Vastus. 64 km kõrgusel on siis õhurõhk mmHg.

Ülesanne 333. Kolmnurga ümbermõõt

Vastus. Kolmnurga K₅ ümbermõõt on cm.

Ülesanne 334. Kuulujutu levitamine

Vastus. Sel ajal saab „uudisest” teada inimest.

Ülesanne 335. Segametsa juurdekasv

Vastus. 10 aasta pärast on metsas tm puitu.

Ülesanne 336. Hoius

Vastus. Hoius kasvab euroni.

Ülesanne 337. India rahvaarv

Vastus. India rahvaarv oleks olnud siis miljardit. Tegelikult oli see miljardit.

Ülesanne 338 .Geomeetriline jada

a_1=1, q=2

a_1=8, q=\frac{1}{2}

a_1=\frac{1}{4}, q=4

Kirjutage välja iga antud jada 6 esimest liiget.
Uurige, kuidas avaldub geomeetrilise jada iga liige (alates teisest) oma kahe naaberliikme kaudu.
Tõestage leitud seos.
Millest võiks olla geomeetriline jada saanud oma nimetuse?
Kas leitud seos kehtib igas geomeetrilises jadas?

Еще на эту тему

Ülesanded B

Ülesanne 339. Geomeetriline jada

Leidke positiivsete liikmetega geomeetrilise jada kolm järjestikust liiget, kui nende summa on 21 ning nende pöördarvude summa on \frac{7}{12}.

Vastus. Need liikmed on ; ; või ; ; .

Ülesanne 340. Geomeetriline jada

Vastus. Selle geomeetrilise jada esimesed liikmed on ; ; ; ; …

Vihje

Koostage kaks võrrandit, tooge teisest võrrandist q³ sulgude ette ja sulgudesse jääva avaldise väärtus asendage esimesest võrrandist.

Ülesanne 341. Risttahuka mõõtmed

Vastus. Risttahuka mõõtmed on m, m ja m.

Ülesanne 342. Neli arvu

Vastus. Need arvud on , , ja .

Ülesanne 343. Neli arvu

Vastus. Need arvud on , , ja .

Ülesanne 344. Kolm arvu

Vastus. Need arvud on , ja või , ja .

Еще на эту тему

Geomeetrilise jada n esimese liikme summa

Legend jutustab, et malemängust vaimustatud India kuningas Sheran tegi oma alamale, malemängu leiutajale, ettepaneku ütelda mingi soov, mille kuningas võiks täita. Leiutaja soov oli järgmine: üks nisutera malelaua 1. ruudu eest, 2 nisutera 2. ruudu eest, 4 nisutera 3. ruudu eest, 8 nisutera 4. ruudu eest, üldiselt iga järgmise ruudu eest kaks korda rohkem teri kui eelmise eest. Kuningas arvas, et see soov on liiga tagasihoidlik. On see nii?Viljaterade arvud malelaual on geomeetrilise jada 1; 2; 4; 8; …; 2^n-1; … liikmed. Terade koguarv oleks selle jada 64 esimese liikme summa1 + 2 + 4 + 8 + … + 2⁶³.Tuletamegi järgnevas valemi geomeetrilise jada n esimese liikme summa arvutamiseks. Tähistame selle summa sümboliga S_n. SeegaS_n = a₁ + a₂ + a₃ + … + a_n ehkS_n = a₁ + a₁q + a₁q² + a₁q³ + … + a₁q^n–1. (1)Korrutame viimast võrdust teguriga q:S_nq = a₁q + a₁q² + a₁q³ + a₁q⁴ + … + a₁qⁿ. (2)Lahutades võrdusest (2) võrduse (1), saameS_nq – S_n = (a₁q + a₁q² + … + a₁qⁿ^–1 + a₁qⁿ) – (a₁ + a₁q + … + a₁q^n–2 + a₁q^n–1).Pärast koondamist võrduse paremal pool saameS_nq – S_n = a₁qⁿ – a₁ ehk S_n(q – 1) = a₁(qⁿ – 1).Kui q – 1 ≠ 0, saame viimasest võrdusest geomeetrilise jada n esimese liikme summa valemi

$S_{n} = \frac{a_{1} (q^{n} - 1)}{q - 1}$ , kus q ≠ 1.

Viimasest valemist saame lihtsa teisenduse teel valemi jada liikmete summa leidmiseks a₁ ja a_n kaudu:

S_n = \frac{a_1q^n-a_1}{q-1} = \frac{a_1q^{n-1}q-a_1}{q-1} = \frac{a_nq-a_1}{q-1} ehk

$S_{n} = \frac{a_{n} q - a_{1}}{q - 1}$ , kus q ≠ 1.

Näide 1.

Lahendame käesoleva peatüki algul esitatud ülesande viljaterade arvust, mis tuleks kuningal malelaua leiutajale anda. Vaadeldavas jadas a₁ = 1, q = 2, n = 64 ja

S_{64} = \frac{1\left(2^{64}-1\right)}{2-1} = 2^{64}-1 = 18\ 446\ 744\ 073\ 709\ 551\ 615.See viljaterade kogus oleks üle triljoni tonni. Võrrelge seda arvu kogu maailma aastase nisutoodanguga.

Näide 2. Leiame summa 1 + x + x² + … + xⁿ^–1, kus x ≠ 1. Liidetavad on geomeetrilise jada liikmed, kus a₁ = 1, q = x. Seega1+x+x^2+\dots+x^{n-1} = \frac{x^n-1}{x-1}.Siit saame, et kehtib valem xⁿ – 1 = (x – 1)(1 + x + … + x^n–1). Kuidas näeb see valem välja n = 2 ja n = 3 korral?

Еще на эту тему

Ülesanded A

Ülesanne 345. Geomeetrilise jada n esimese liikme summa

Ülesanne 346. Geomeetrilise jada n esimese liikme summa

a₁ = 3, q = 2, n = 5

Vastus. S_n =

a₁ = 4, q = 0,5, n = 6

Vastus. S_n =

a₁ = 0,5, q = 3, n = 4

Vastus. S_n =

a₁ = 5, q=\frac{-1}{2}, n = 10

Vastus. S_n =

Ülesanne 347. Geomeetrilise jada n esimese liikme summa

3, –6, 12, …

Vastus. S₆ =

58; 87; 130,5; …

Vastus. S₆ =

3, 6, 12, …

Vastus. S₆ =

1, \frac{1}{2}, \frac{1}{4}, …

Vastus. S₆ =

Ülesanne 348. Geomeetrilise jada n esimese liikme summa

Vastus. Selles jadas tuleb võtta liiget.

Ülesanne 349. Geomeetrilise jada n esimese liikme summa

Vastus. Selles jadas tuleb võtta liiget.

Ülesanne 350. Summa leidmine

1 + 3 + 3² + … + 3⁸ =

2⁹ + 2⁸ + … + 2 + 1 =

1+\frac{1}{2}+\frac{1}{4}+\dots+\frac{1}{2^7} =

1 – 2 + 2² – 2³ + … + 2¹² =

1 + x + x² + … + x¹⁰⁰ =

1 – x + x² – x³ + … – x¹⁵ =

Ülesanne 351. Kummipall

Vastus. Kummipall on läbinud siis ligikaudu m.

Ülesanne 352. Kuulujutu levitamine

Vastus. Kell 15⁰⁰ on „uudist” kuulnud inimest.

Ülesanne 353. Postkaardimäng

Vastus. Aasta viimasel esmaspäeval saadetaks teele postkaarti. Kogu aasta jooksul osaleks selles mängus postkaarti.

Ülesanne 354. Linna elanike arv

Vastus. Linna elanike arvu aastane kasvutegur on . Linna elanike arv 5 aasta pärast on .

Еще на эту тему

Ülesanded B

Ülesanne 355. Kolm arvu

Vastus. Need arvud on , ja või , ja .

Ülesanne 356. Kolm arvu

Vastus. Need arvud on , ja .

Ülesanne 357. Kolmekohaline arv

Vastus. See arv on .

Ülesanne 358. Kolm arvu

Vastus. Need arvud on , ja või , ja .

Еще на эту тему

Hääbuva geomeetrilise jada summa

Õpiku järgnevates osades on tihti tegemist selliste jadadega, mille liikmed lähenevad nullile, kui jadas järjest kaugemale minna. Nendele jadadele on antud omaette nimetus.

Jada nimetatakse hääbuvaks ehk nullile lähenevaks, kui jadas järjest kaugemale minnes selle jada liikmed erinevad arvust 0 kui tahes vähe.

Lühemalt saab hääbuvat jada kirjeldada järgmiselt: kui n\to∞, siis a_n\to0 (loetakse nii: kui n läheneb lõpmatusele, siis a_n läheneb nullile).

Ülesanne 359. Hääbuv geomeetriline jada

1;\ \frac{1}{2};\ \frac{1}{3};\ \frac{1}{4};\ \dots
10; 9; 8; 7; …

5;\ \frac{5}{3};\ \frac{5}{9};\ \frac{5}{27};\ \dots
2;\ -1;\ \frac{1}{2};\ -\frac{1}{4};\ \dots

Leidke iga antud jada üldliige.

Jada	1)	2)	3)	4)
Jada üldliige	a_n =	a_n =	a_n =	a_n =

Missugused antud jadadest on geomeetrilised?

1)
2)
3)
4)

Missugused antud jadadest on hääbuvad?

1)
2)
3)
4)

Missugused antud jadadest on hääbuvad ja geomeetrilised? Leidke nende jadade tegurid.
Tooge veel näiteid hääbuvatest geomeetrilistest jadadest.

Geomeetriline jada on hääbuv, kui |q| < 1.

Näide 1. Vaatleme hääbuvat geomeetrilist jada

1;\ \frac{1}{2};\ \frac{1}{4};\ \frac{1}{8};\ ...;\ \left(\frac{1}{2}\right)^{n-1};\ ....

Joon. 2.7

Kujutame selle jada esimesed liikmed arvteljel (joonis 2.7). Mida kaugemale me jadas läheme, seda enam lähenevad jada liikmed nullile. Näiteksa_{10}=\left(\frac{1}{2}\right)^9=0,00195, a_{16}=\left(\frac{1}{2}\right)^{15}=0,0000305, a_{21}=\left(\frac{1}{2}\right)^{20}=0,000000954.Leidke arvutil a₃₁, a₄₁, a₁₀₀ ja veenduge, et kui n\to∞, siis a_n\to0.Need nullilähedase väärtusega liikmed ei mõjuta oluliselt jada n esimese liikme summat S_n. Arvutame antud jada n esimese liikme summa:S_n=\frac{1\cdot\left[\left(\frac{1}{2}\right)^n-1\right]}{\frac{1}{2}-1} = \frac{1-\left(\frac{1}{2}\right)^n}{\frac{1}{2}} = 2-\left(\frac{1}{2}\right)^{n-1}.

Kui n on küllalt suur, läheneb summa S_n järjest enam arvule 2 (vt ka juuresolevat tabelit):

See tähelepanek annab meile aluse lugeda lõpmata paljude liidetavatega summa1+\frac{1}{2}+\frac{1}{4}+\dots+\frac{1}{2^{n-1}}+\dotslõplikuks väärtuseks 2.

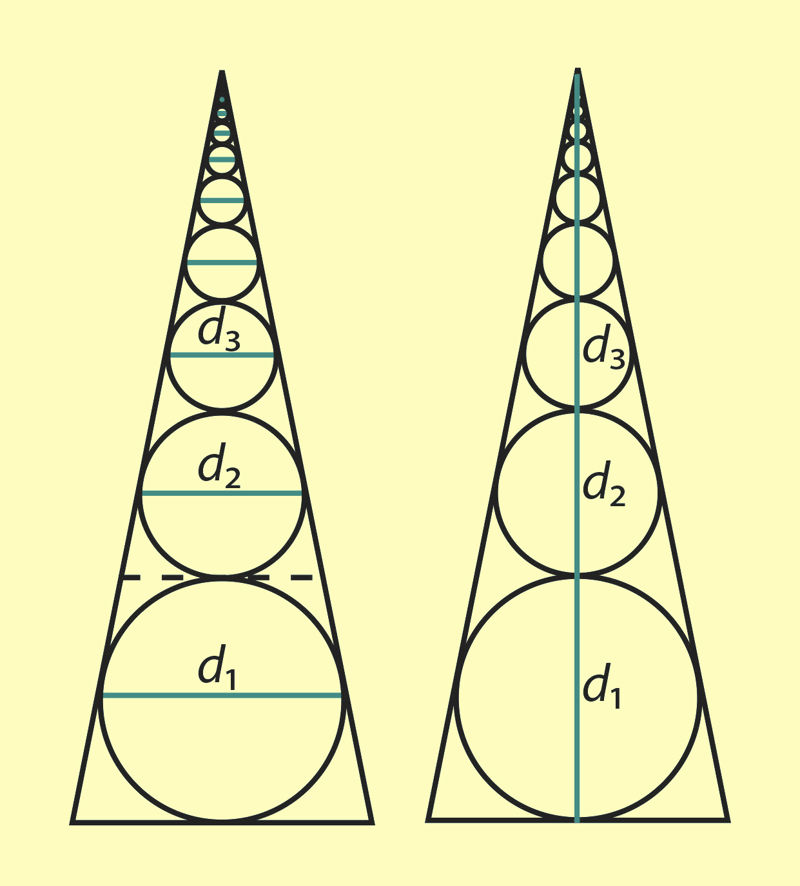
Joon. 2.8

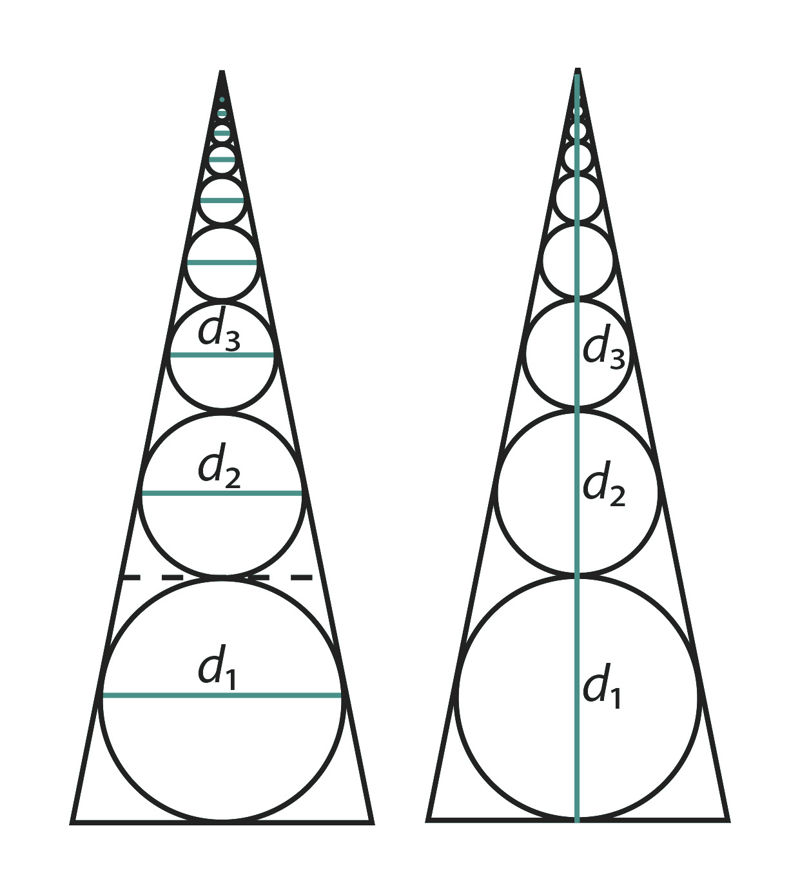
Analoogiliselt näitega 1 võime arutleda mis tahes hääbuva geomeetrilise jada korral ja saada tema liikmete summaks lõpliku arvu. Öeldut illustreerib ka joonis 2.8. Kõigepealt joonestame vasakpoolsesse võrdhaarsesse kolmnurka siseringjoone. Olgu selle diameeter d₁. Tõmmates mõttes sellele ringjoonele kolmnurga alusega paralleelse puutuja, tekib esialgse kolmnurgaga sarnane kolmnurk. Joonestame ka sellesse kolmnurka siseringjoone, mille diameeter olgu d₂. Sellist protsessi võib lõpmatult jätkata. Nii tekib meil ringjoonte jada, kusjuures diameetrite pikkused moodustavad hääbuva geomeetrilise jada d₁, d₂, d₃, … .

Kujutame parempoolsel joonisel diameetrid d₁, d₂, d₃, ... risti kolmnurga alusega. Lihtne on näha, et diameetrite pikkuste summa d₁ + d₂ + d₃ + … + d_n + … on lõplik ja võrdub esialgse kolmnurga kõrgusega.Vaatleme, kuidas on võimalik arvutada mis tahes hääbuva geomeetrilise jada liikmete summat a₁ + a₂ + a₃ + … + a_n + …. Selleks teisendame geomeetrilise jada n esimese liikme summa valemit järgmiselt:S_n=\frac{a_nq-a_1}{q-1}=\frac{a_nq}{q-1}-\frac{a_1}{q-1}.Teame, et hääbuva jada korral a_n\to0, kui n\to∞. Seega ka liige \frac{a_nq}{q-1}\to0 ja summast jääb alles vaid teine liidetav -\frac{a_1}{q-1}=\frac{a_1}{1-q}.

Avaldist $\frac{a_{1}}{1 - q}$ nimetatakse hääbuva geomeetrilise jada (a_n) summaks ning tähistatakse tähega S.

$S = \frac{a_{1}}{1 - q}$ .

Seega S on arv, millele läheneb hääbuva geomeetrilise jada n esimese liikme summa S_n, kui jada liikmete arv n tõkestamatult kasvab.

Näide 2

Leiame hääbuva geomeetrilise jada 5; 3; \frac{9}{5}; …; 5\cdot\left(\frac{3}{5}\right)^{n-1}; ... 7 esimese liikme summa ja jada summa. Selles jadas a₁ = 5, q = 0,6.

S_7=\frac{5\left(0,6^7-1\right)}{0,6-1}\approx12,15 ja S=\frac{5}{1-0,6}=12,5.

Näide 3.

Teisendame lõpmatu perioodilise kümnendmurru 0,(13) harilikuks murruks. Teame, et 0,(13) = 0,131313… = 0,13 + 0,0013 + + 0,000013 + …. Paremal olevad liidetavad on hääbuva geomeetrilise jada järjestikused liikmed, kusjuures q=\frac{0,0013}{0,13}=\frac{0,000013}{0,0013}=0,01<1 ja a₁ = 0,13.

Seega S=\frac{0,13}{1-0,01}=\frac{0,13}{0,99}=\frac{13}{99}.

Vastus. 0,\left(13\right)=\frac{13}{99}.

Еще на эту тему