Vaatleme funktsioone, mis kirjeldavad mingi protsessi muutumist sõltuvalt ajast. Mitmete muude faktorite kõrval võib ajast sõltuda näiteks:
- keha poolt läbitud tee pikkus;
- tilkuva õlireservuaari poolt tekitatava õlilaigu pindala;
- auto vigastatud õhukummi ruumala kummi tühjenedes jne.
Nagu nägime peatükis 4.6, väljendab selliste funktsioonide tuletis antud kohal protsessi muutumise hetkkiirust vastaval ajahetkel t0:
kus f ja v on funktsioonid, mis kirjeldavad vastavalt protsessi muutumist ning selle protsessi muutumise hetkkiirust sõltuvalt ajast t. Seega, kui keha poolt aja t jooksul läbitud teepikkust kirjeldab funktsioon s (t), siis avaldub selle keha kiirus hetkel t seosega:
v (t) = s'(t).
Kui leida siit nüüd v'(t), saame valemi kiiruse muutumise kiiruse ehk kiirenduse a (t) arvutamiseks:
a (t) = v'(t).
Näide 1.
Sirgjooneliselt liikuva keha asukoht sirgel on määratud valemiga s (t) = –0,25t2 + 4t, kus s (t0) on keha koordinaat sellel sirgel hetkel t0.
Sellisel juhul öeldakse, et keha liigub sirgjooneliselt seaduse s (t) järgi.
Leiame:
- valemid selle keha kiiruse ja kiirenduse arvutamiseks suvalisel hetkel;
- keha kiiruse ja kiirenduse hetkel t0 = 2;
- mitme sekundi pärast jääb keha seisma.
Leiame esmalt valemid kiiruse ja kiirenduse arvutamiseks suvalisel hetkel:
Arvutame nüüd kiiruse hetkel
Keha kiirendus on konstantne, olles hetkel
Hetkel, mil keha jääb seisma, on tema kiirus null. Seega lahendades võrrandi
saame vastuse ka viimasele küsimusele: keha jääb seisma 8 sekundi möödudes.
Joonestame nüüd arvutil (näiteks programmiga GeoGebra) mõlema saadud funktsiooni graafikud ühes ja samas teljestikus. Olgu horisontaalteljel aeg ja vertikaalteljel kas keha kaugus lähtepunktist või siis kiirus (joonis 5.1).
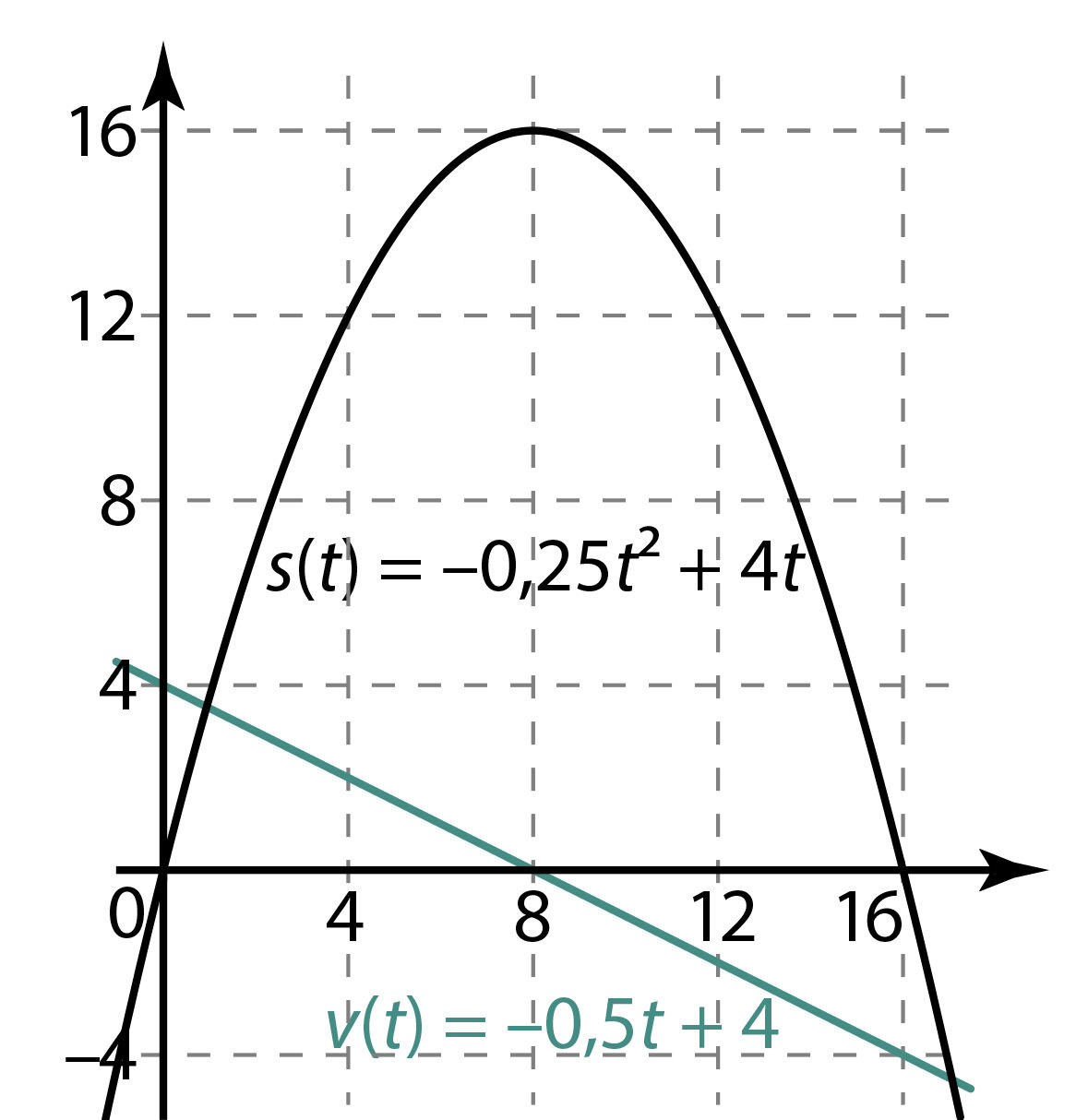 Joon. 5.1 | ||||||
Graafikutelt võime lugeda järgmist:
- kaheksa esimest sekundit keha kaugeneb lähtepunktist (kaugus lähtepunktist kasvab);
- kaheksandal sekundil on keha lähtepunktist kõige kaugemal (16 m) ja jääb hetkeks seisma;
- seejärel hakkab keha taas lähtepunktile lähenema ja jõuab sinna kuueteistkümnendal sekundil;
- keha kiirus on liikumise alghetkel
4\ \frac{\mathrm{m}}{\mathrm{s}} .
Edasi kiirus kahaneb kuni keha seisma jäämiseni kaheksandal sekundil. Seejärel omab kiirus negatiivseid väärtusi. See tähendab, et keha liigub kaugust kirjeldava teljega vastassuunaliselt.
Näide 2.
Sirgjooneliselt liikuva keha asukoht sirgel on määratud valemiga
Leiame selle keha liikumise kiiruse hetkel, kui tema kiirendus on null.
Leiame valemid keha kiiruse ja kiirenduse arvutamiseks.
Võrrandist
Vastus. Ajahetkel, mil antud keha kiirendus on null, on tema kiirus
Näide 3.
Õlireservuaarist mahavalguv õli moodustab ringikujulise laigu, mille raadius kasvab konstantse kiirusega
Olgu t lekke kestus sekundites, r ja S vastavalt õlilaigu raadius sentimeetrites ning õlilaigu pindala ruutsentimeetrites pärast t sekundit väldanud leket. Pindala muutumise kiirus v avaldub sel juhul valemiga
Et õlilaigu raadius on ise aja t funktsioon, siis on meil tegemist liitfunktsiooniga. Vastavalt liitfunktsiooni diferentseerimise reeglile saame nüüd, et
Ülesande tingimuste kohaselt on laigu raadiuse muutumise kiirus
Et arvutada õlilaigu pindala kasvamise kiirust hetkel, kui laigu raadius on 18 cm, leiame saadud tuletisfunktsiooni väärtuse kohal r = 18:
v =
Vastus. Ajahetkel, kui õlilaigu raadius on 18 cm, kasvab selle pindala kiirusega
Näide 4.
Viie meetri pikkune redel (joonis 5.2) libiseb mööda majaseina alla nii, et redeli alumine ots eemaldub seinast konstantse kiirusega
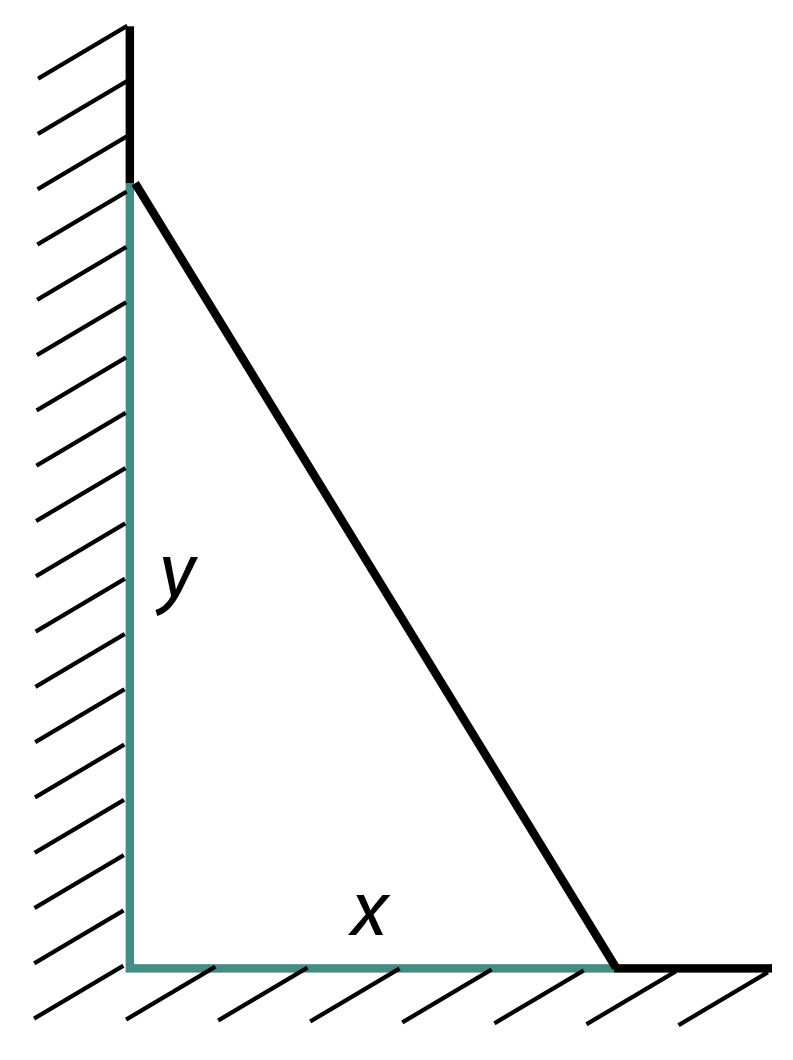 Joon. 5.2 | ||||||
Olgu t aeg sekundites redeli libisemise algusest, x ja y vastavalt redeli alumise otsa kaugus majaseinast ning ülemise otsa kaugus maapinnast. Kasutades Pythagorase teoreemi, avaldame y muutuja x funktsioonina:
Leiame nüüd valemi muutuja y hetkkiiruse
v =
Arvestades seost 1, saame siit, et
Ülesande tingimustele vastavalt x = 3 ja seega y = 4 (seosest 1). Arvestades veel seda, et
v =
Miinusmärk tulemuses näitab, et muutuja x kasvades muutuja y väärtused kahanevad.
Vastus. Redeli ülemise otsa langemise hetkkiirus nõutud hetkel on
Ülesanded A
Ülesanne 907. Liikumise kiirus ja kiirendus
Leidke
- liikumise kiirus hetkel
t_1=3 jat_2=5,6 .
Vastus. Kuit_1=3 , siis v =\frac{\mathrm{m}}{\mathrm{s}} ja kuit_2=5,6 , siis v =\frac{\mathrm{m}}{\mathrm{s}} . - kiirendus mõlemal nimetatud ajahetkel.
Vastus. Kuit_1=3 , siis a =\frac{\mathrm{m}}{\mathrm{s}^2} ja kuit_2=5,6 , siis a =\frac{\mathrm{m}}{\mathrm{s}^2} .
Ülesanne 908. Liikumise kiirus ja kiirendus
- Leidke punkti kiirus ja kiirendus hetkel t = 5.
Vastus. v (5) =\frac{\mathrm{m}}{\mathrm{s}} , a (5) =\frac{\mathrm{m}}{\mathrm{s}^2} . - Millisel hetkel on punkti liikumise kiirendus null?
Vastus. Liikumise kiirendus on null, kui t = . - Joonestage arvutil funktsioonide s (t) ja v (t) graafikud ning kirjeldage nende abil punkti liikumist esimese nelja sekundi jooksul (kaugus lähtepunktist, kiiruse ja kiirenduse muutumine).
Ülesanne 909. Liikumise kiirus ja kiirendus
- Leidke punkti liikumise hetkkiirus ja kiirendus liikumise teise sekundi lõpul.
Vastus. Teise sekundi lõpul on punkti liikumise hetkkiirus\frac{\mathrm{m}}{\mathrm{s}} ja kiirendus\frac{\mathrm{m}}{\mathrm{s}^2} . - Mitmenda sekundi lõpul jääb punkt seisma?
Vastus. Punkt jääb seisma sekundi lõpul. - Joonestage arvutil funktsioonide s (t) ja v (t) graafikud ning kirjeldage nende abil punkti liikumist esimese nelja sekundi jooksul (kaugus lähtepunktist, kiiruse ja kiirenduse muutumine).
Ülesanne 910. Langemise kiirus ja kiirendus
Leidke
- mitmendal sekundil põrkub pakk maaga.
Vastus. Pakk põrkub maaga sekundil. - paki kukkumise kiirus ja kiirendus langemise 4. sekundi lõpul.
Vastus. 4. sekundi lõpul on paki kukkumise kiirus\frac{\mathrm{m}}{\mathrm{s}} ja kiirendus\frac{\mathrm{m}}{\mathrm{s^2}} . - ajahetk, millal pakk põrkub maaga.
Vastus. Ajahetk, millal pakk põrkub maaga on s.
Ülesanne 911. Langemise kiirus ja kiirendus
- Kui sügav on kraater, kui kivi langes kraatri põhja 10 sekundiga?
Vastus. Kraatri sügavus on meetrit. - Kui suur on kivi liikumise kiirus põhja jõudmise hetkel?
Vastus. Kivi liikumise kiirus põhja jõudmise hetkel on\frac{\mathrm{m}}{\mathrm{s}} .
Ülesanne 912. Bakterite arvu muutumine
- Kui suur oli bakterite lähtearv biomassis?
Vastus. Bakterite lähtearv biomassis oli . - Kui suur on bakterite juurdekasv ajamomendil t = 3,5 min?
Vastus. Bakterite juurdekasv ajamomendil t = 3,5 min, oli bakterit minutis.
Ülesanded B
Ülesanne 913. Palli liikumine
- Kui kõrgelt pall visati?
Vastus. Pall visati m kõrguselt. - Kui suur oli palli liikumise algkiirus?
Vastus. Palli liikumise algkiirus oli\frac{\mathrm{m}}{\mathrm{s}} . - Kas pall visati üles või alla?
Vastus. Pall visati . - Mitu sekundit pärast viset asus pall maapinnast kõige kõrgemal ja kui kõrgel?
Vastus. Pall asus maapinnast kõige kõrgemal sekundi pärast ja siis oli pall m kõrgusel. - Mitu sekundit pärast viset kukkus pall maha?
Vastus. Pall kukkus maha sekundit pärast viset. - Kui suur oli palli kiirus mahakukkumise hetkel?
Vastus. Mahakukkumise hetkel oli palli kiirus\frac{\mathrm{m}}{\mathrm{s}} .
Ülesanne 914. Kahe punkti liikumine
Vastus. Esimese punkti kiirus on teise omast suurem, kui t ∈
Ülesanne 915. Õli valgumine
Õli valgub purunenud laevalt veepinnale, moodustades seal ringikujulise laigu, mille pindala kasvab konstantse kiirusega
Vastus. Selle ringi raadius kasvab sel hetkel kiirusega
Ülesanne 916. Tuletõrjeredeli libisemine
13 meetri pikkune tuletõrjeredel libiseb mööda seina nii, et tema ülemine ots liigub otse alla ühtlase kiirusega
Vastus. Redeli alumine ots kaugeneb majaseinast siis kiirusega
Ülesanne 917. Kuubi ruumala kasvamine
Hetkel, kui kuubi ruumala kasv on
Vastus. Kuubi täispindala kasvab siis kiirusega
Ülesanne 918. Silindri mõõtmete muutumine
Hetkel, kui silindri diameeter kasvab kiirusega
Vastus. Silindri ruumala jääb muutumatuks, kui kõrguse muutumise kiirus on
Ülesanne 919. Nakkushaiguse levik
Vastus. Haigestumisprotsendi kasvamise kiirus saavutab maksimumi päeval.
Ülesanne 920. Paatide liikumine
Ühe paadi kiirus on
Vastus. Kümne minuti pärast on paadid teineteisest m kaugusel ja nad eemalduvad kiirusega
Ülesanne 921. Putukate liikumine
Esimene neist liigub ühtlaselt kiirusega

Vastus. Liikumise 2. minuti lõpul eemalduvad putukad teineteisest kiirusega
