Ülesanne 976. Aia rajamine
Tähistame aia pikkuse ja pindala vastavalt tähtedega x ja y (joonis 5.12). Et aia laius on 100 – x, siis avaldub aia pindala y muutuja x funktsioonina järgmiselt: y = x(100 – x).
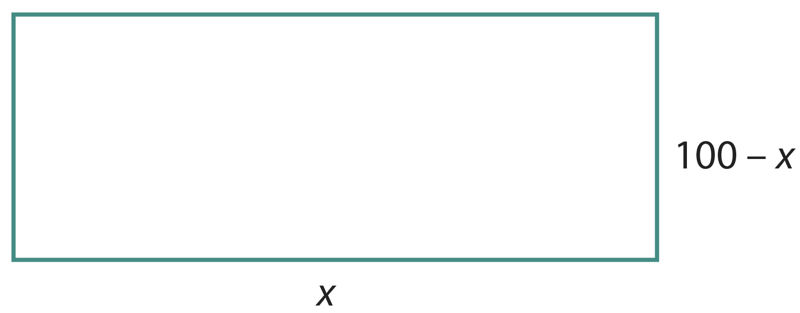
Seega taandub antud ülesanne argumendi nende väärtuste leidmisele, mille korral vaadeldaval funktsioonil on maksimaalne väärtus. Kuidas neid leida?
NB!
Ekstreemum on ühine nimetus maksimumile ja miinimumile.
Ekstreemum ye on funktsiooni väärtus.
Ekstreemumkoht xe on argumendi väärtus.
Ekstreemumpunkt on punkt, mille koordinaadid on ekstreemumkoht ja ekstreemum.
Jooniselt 5.13 (a ja b) näeme, et kui diferentseeruval funktsioonil on kohal x0 maksimum või miinimum, siis on tema graafiku puutuja sellel kohal paralleelne x-teljega, s.t f ′(x0) = 0. Samas selgub, et tuletis võib olla võrdne nulliga ka kohal, kus funktsioonil pole ekstreemumit (joonis 5.13c).
Seega
funktsioonil y = f (x) võib ekstreemum olla kohal, kus tema tuletis on võrdne nulliga.
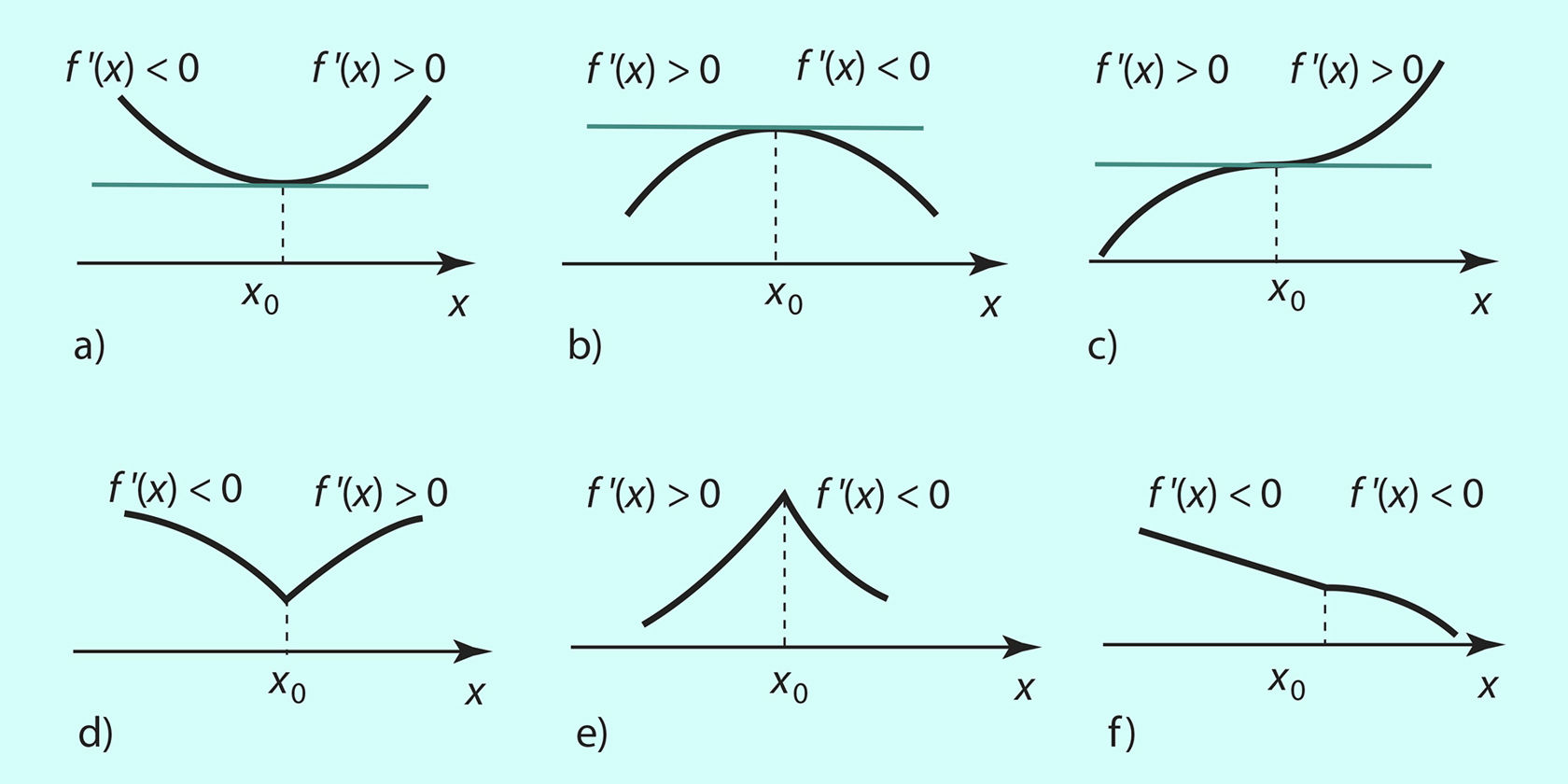
Veel näeme samalt jooniselt (d ja e), et
funktsioonil y = f (x) võib ekstreemum olla ka kohal, kus tal tuletis puudub.
Mis on aga vältimatult vajalik selleks, et tuletise nullkoht või argumendi see väärtus, kus tuletis puudub, oleks funktsiooni ekstreemumkoht? Jooniselt 5.13 (a, b, d ja e) nähtub, et kohal, kus funktsioonil on ekstreemum, läheb kasvamine üle kahanemiseks või kahanemine üle kasvamiseks, s.t funktsiooni tuletis muudab ekstreemumkohal märki.
Seega tuleb funktsiooni y = f (x) ekstreemumkohtade leidmiseks välja selgitada funktsiooni tuletise nullkohad ja kohad, kus tuletis puudub.
Kui leitud kohal funktsiooni tuletis muudab märki, siis on tegemist ekstreemumkohaga.
Kui kasvamine läheb leitud kohal üle kahanemiseks, on antud koht maksimumkoht, vastasel juhul aga miinimumkoht.
Kui leitud kohal tuletis märki ei muuda, siis funktsioonil pole sellel kohal ekstreemumit.
Sageli on tarvis leida funktsiooni suurim või vähim väärtus etteantud lõigus. Taolistel juhtudel tuleb silmas pidada veel seda, et lõigus määratud funktsioonil võib ekstremaalne väärtus olla ka lõigu otspunktides (joonis 5.14).
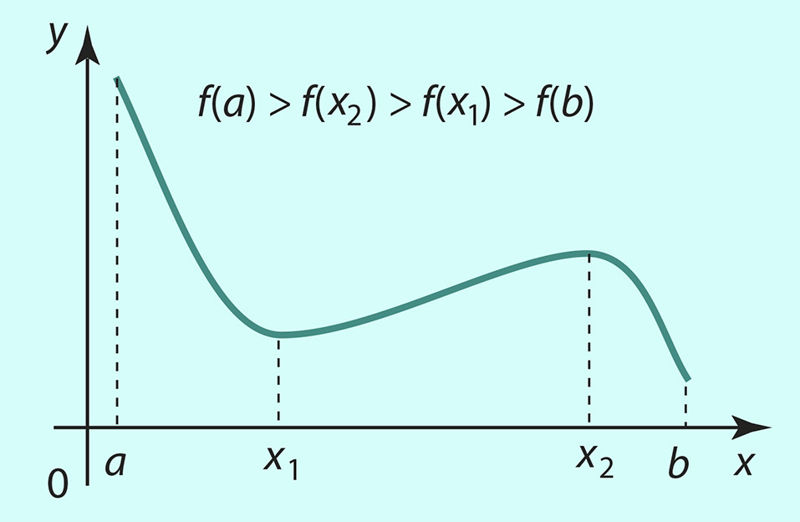
Seega juhul, kui funktsiooni ekstreemumit otsitakse mingis lõigus, tuleb lisaks ekstreemumkohtadele vaatluse alla võtta ka vaadeldava lõigu otspunktid. Kõigi nende argumendi väärtuste korral arvutatakse funktsiooni vastavad väärtused ja viimaste seast leitakse siis vastavalt vajadusele kas suurim või vähim.
Näide 1.
Leiame funktsiooni
Leiame esmalt funktsiooni kõik ekstreemumkohad vahemikust (–∞; ∞). Et vaadeldav funktsioon on selles vahemikus diferentseeruv, siis võivad tema ekstreemumid olla vaid tuletise nullkohtades.
Võrrandist
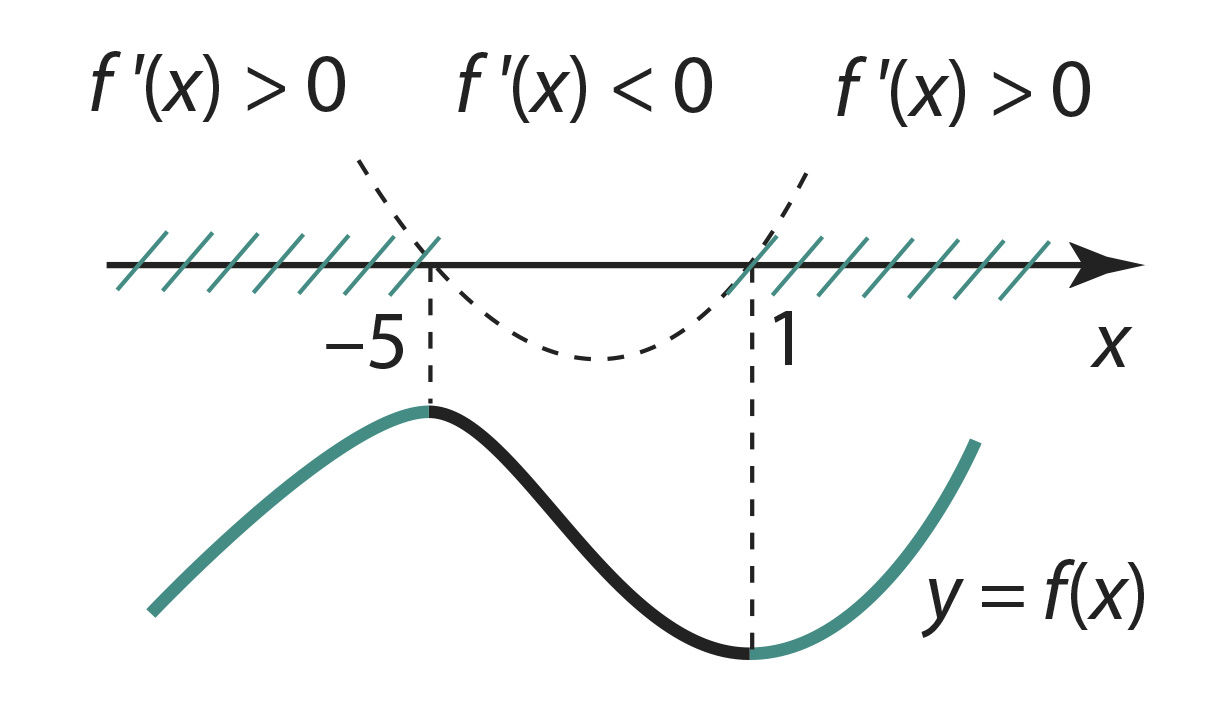 Joon. 5.15 | ||||||
Skitseerides tuletise märgi muutused joonisel (joonis 5.15), näeme, et funktsioonil
Lõpuks leiame funktsiooni ekstreemumid, s.o y (–5) ja y (1):
Vastus. Funktsioonil
Näide 2.
Leiame funktsiooni
Ekstreemumkohti otsime nüüd funktsiooni tuletise nullkohtades ja antud lõigu otspunktides. Lahendame esmalt võrrandi y' = 0. Võrrandist
2x – 8 = 0 saame, et x = 4.
Kontrollime nüüd, kas argumendi saadud väärtus kuulub lõiku [2; 7]. Vastus on jaatav. Eitava vastuse korral jääks see väärtus edasiste vaatluste alt välja. Leiame seejärel funktsiooni väärtused tuletise nullkohas ja lõigu [2; 7] otspunktides. Et y (4) = –1, y (2) = 3 ja y (7) = 8, siis on funktsiooni suurim ja vähim väärtus antud lõigus vastavalt 8 ja –1.
Vastus. Funktsioon
Näide 3.
Lahendame lõpuni ülesande 976.
Antud juhul otsime ekstreemumkohta funktsiooni
Võrrandist
Et funktsioon y = x(100 – x) on x < 50 korral kasvav (y' > 0) ja x > 50 korral kahanev (y' < 0), siis on tal sellel kohal maksimum. Siit näemegi, et vaadeldaval funktsioonil on kohal x = 50 maksimum.
Vastus. Aed tuleb teha ruudukujuline 50 m pikkuse küljega.
Näide 4.
Leiame funktsiooni y = x2 – 2|x| kõik ekstreemumid lõigus [–3; 4].
Antud funktsiooni võime esitada kujul
, millest
Et funktsioon y = x2 – 2|x| on pidev lõigus [–3; 4] ja tal puudub tuletis kohal x = 0 (tuletisfunktsioon on sellel kohal katkev, vt joon. 5.16), siis otsime ekstreemumkohti tuletise nullkohtades, lõigu [–3; 4] otspunktides ja kohal, kus funktsioonil tuletis puudub. Seega xe ∈ {–3; –1; 0; 1; 4}.
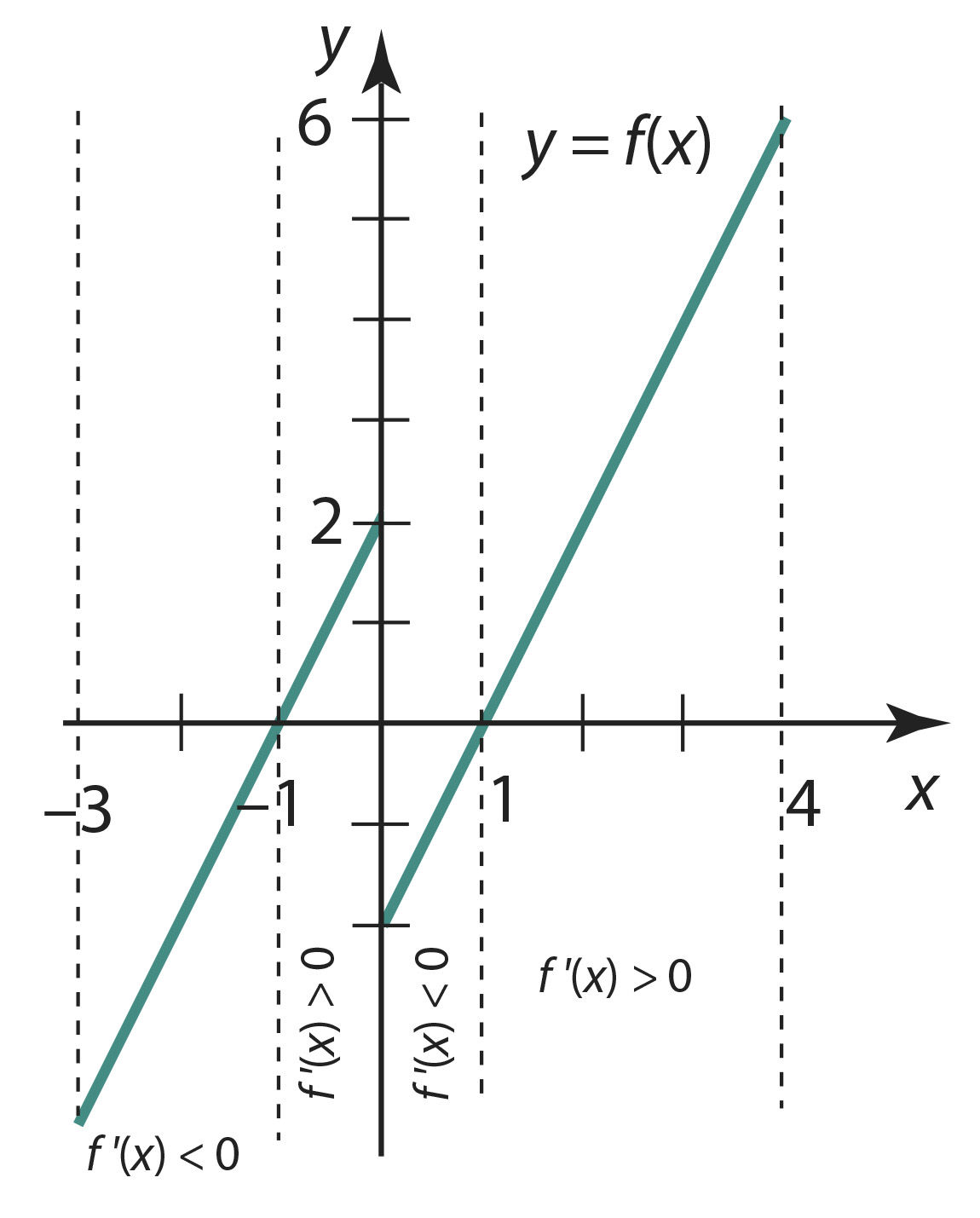 Joon. 5.16 | ||||||
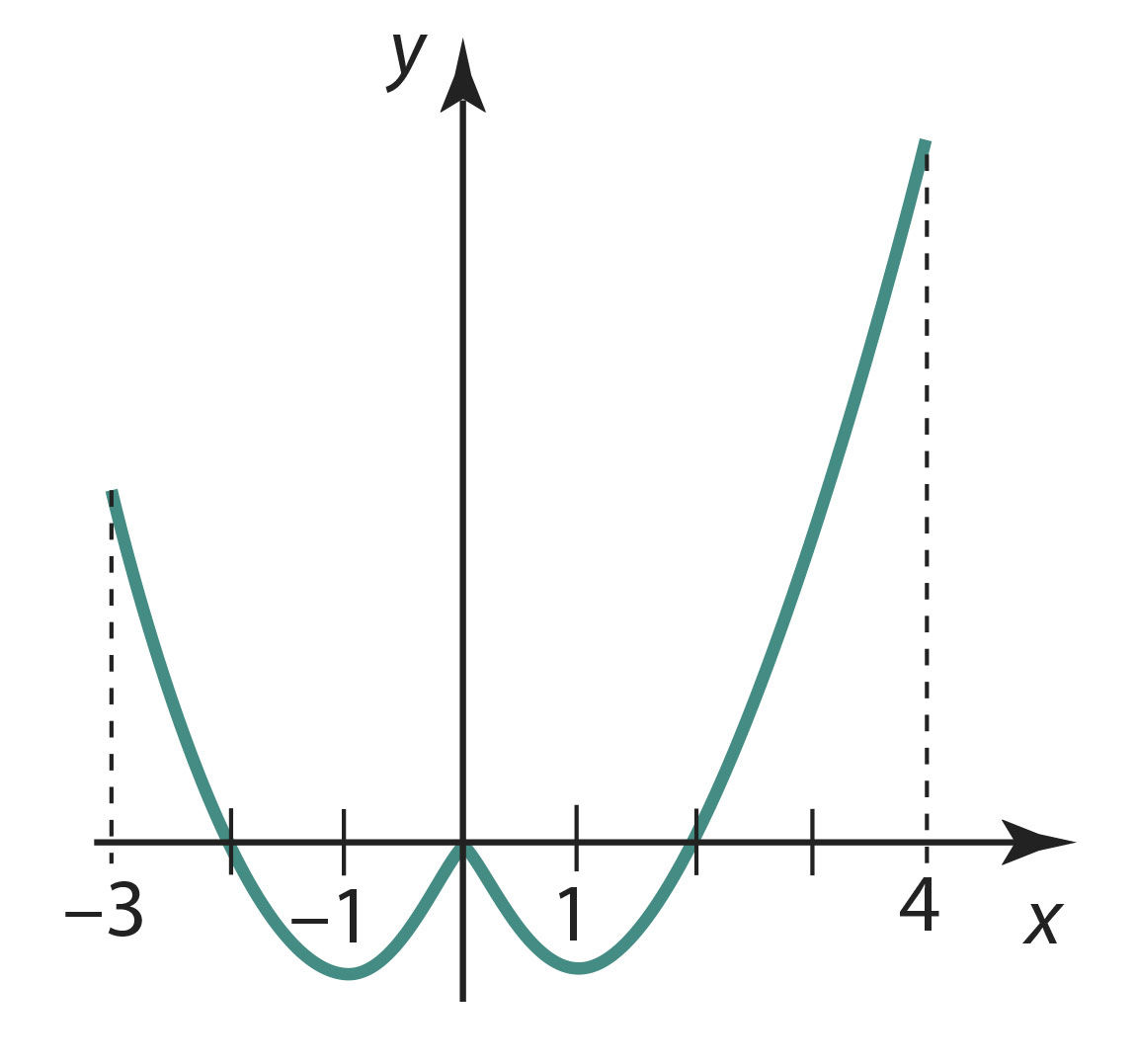 Joon. 5.17 | ||||||
Jälgides funktsiooni tuletise märgimuutusi ja funktsiooni väärtusi võimalikes ekstreemumkohtades (joonised 5.16 ja 5.17) saame, et vaadeldaval funktsioonil on maksimum kohtadel x1 = –3, x2 = 0 ja x3 = 4 ning miinimum kohtadel x4; 5 = ±1. Seega, maksimumid on y (–3) = 3, y (0) = 0, y (4) = 8 ja miinimumid on y (±1) = –1.
Vastus. Funktsioonil y = x2 – 2|x| on lõigus [–3; 4] kolm maksimumi 3; 0 ja 8 ning kaks miinimumi, kumbki –1.
Ülesanded A
Ülesanne 977. Funktsiooni ekstreemumkohad ja ekstreemumid
Ülesanne 978. Auto bensiinikulu
Vastus. Siis tuleks sõita kiirusega
Ülesanne 979. Nakkushaiguse levimine
Vastus. Nakkus saavutab maksimumi . ööpäeval. Sellel päeval on haigestunud % elanikest.
Ülesanne 980. Nõudlus teatud toote järele
Nõudlus teatud toote järele muutub vastavalt seadusele
Mitmendal päeval on nõudlus selle toote järele suurim ja kui suur see siis on?
Vastus. Nõudlus selle toote järele on suurim . päeval, mil see on .
Ülesanne 981. Punkti liikumine mööda sirget
Punkt liigub mööda sirget vastavalt seadusele
- Leidke hetk, millal selle punkti liikumise kiirus on suurim.
Vastus. Punkti liikumise kiirus on suurim, kui t = . - Võrrelge saadud kiirust punkti kiirustega ajahetketel t = 4 ja t = 10. Milline neist kolmest on suurim?
Ülesanded B
Ülesanne 982. Funktsiooni ekstreemumkohad ja ekstreemumid
y = ln x, x > 0
Ülesanne 983. Ekstreemumid antud lõigus
Ülesanne 984. Funktsiooni suurim ja vähim väärtus antud lõigus
Ülesanne 985. Funktsiooni suurim ja vähim väärtus antud lõigus
Ülesanne 986. Parameetri väärtus
Vastus. a =
Ülesanne 987. Parameetrite väärtused
Vastus. a = ; b =
Ülesanne 988. Parameetrite väärtused
Vastus. a = ; b =
Ülesanne 989. Parameetri väärtus
Vastus. a ∈
