Tasandi võrrand rihi kaudu

Riht
Komplanaarsuse kasutamine
Tasandi võrrandi koostamine punkti ja rihi abil
Tasandi võrrandi koostamine kolme punkti abil

Komplanaarsed vektorid

Tasandi võrrandi leidmiseks kasutatakse vektorite komplanaarsust. Kui on teada kaks mittekollineaarset tasandi rihivektorit, siis mis tahes muu selle tasandi vektor on komplanaarne rihivektoritega.

Et tasand oleks üheselt määratud, peab teadma ka vähemalt ühte punkti.

Märka

Kolm võimalust tasandi määramiseks:

üks punkt ja kaks mittekollineaarset vektorit;
kaks punkti ja üks vektor, mis pole paralleelne punkte läbiva sirgega;
kolm punkti, mis ei asu ühel sirgel.

More like this

Punkt ja kaks vektorit

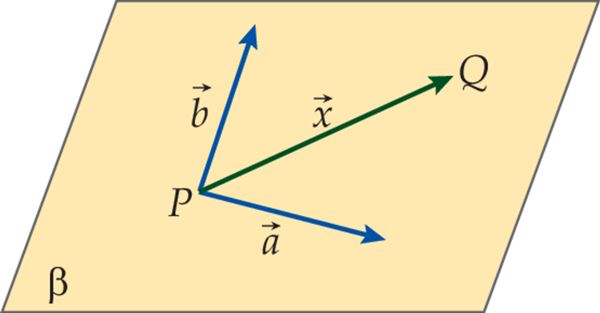
Olgu teada tasandi punkt P(x₀; y₀; z₀) ja kaks rihivektorit
$\vec{a} =$ (a₁; a₂; a₃) ja $\vec{b} =$ (b₁; b₂; b₃).
Võtame tasandil suvalise punkti Q(x; y; z).Siis vektor

$\vec{P Q} =$ (x–x₀; y–y₀; z–z₀)

ja $\vec{a}$ , $\vec{b}$ ja $\vec{P Q}$ on komplanaarsed. Kasutame kolme vektori komplanaarsuse tingimust kolmerealise determinandi kujul:

$|\begin{matrix} x - x_{0} & y - y_{0} & z - z_{0} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}| = 0$ .

Võrrand on determinandi kujul ja selle saab teisendada üldkujule näiteks Sarruse reegli põhjal või mõne teise meetodiga.

Kui tasand läbib punkti P(x₀; y₀; z₀) ja kahte mittekollineaarset vektorit,

$\vec{a} =$ (a₁; a₂; a₃) ja $\vec{b} =$ (b₁; b₂; b3),

siis selle tasandi võrrand on

$|\begin{matrix} x - x_{0} & y - y_{0} & z - z_{0} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}| = 0 .$

Lahendus

Q(x; y; z) on suvaline punkt tasandil.
$\vec{M Q}$ = (; ; ) on vektor tasandil.
Koostame võrrandi

$|\begin{matrix} x - 2 & y - 4 & z - 5 \\ - 1 & 1 & 3 \\ 3 & 1 & - 1 \end{matrix}| = 0,$

seega

–1(x – 2) + 9(y – 4) – (z – 5) –

–3(z – 5) – (y – 4) – 3(x – 2) = 0

–4x + 8y – 4z – = 0.

Taandame võrrandi (–4)-ga.

Vastus

Otsitav võrrand on =0.

Tasand on antud punktiga A(4; –2; 3) ning kahe rihivektoriga (3; 2; –5) ja (1; –2; –5).

Selle tasandi normaalvektor saab olla

(5; 0; 1).
(10; –5; 4).
(–20; 10; –8).
(–1; –1; –1).

Selle tasandi punktid on veel

(5; 0; 3).
(2; –10; 2).
(3; 2; 10,5).

More like this

Kaks punkti ja vektor

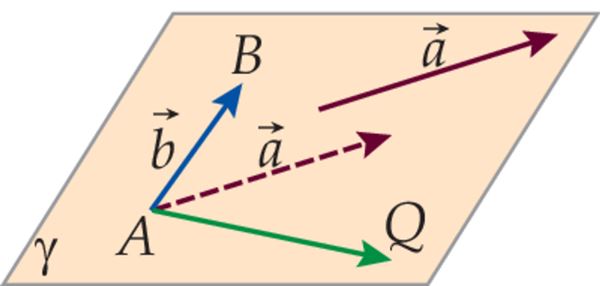
Olgu teada tasandil kaks punkt A(x₁; y₁; z₁) ja B(x₂; y₂; z₂) ning rihivektor $\vec{a} =$ (a₁; a₂; a₃). Võtame tasandil suvalise punkti Q(x; y; z).

Siis võtame teiseks rihivektoriks vektori $\vec{A B}$ või selle vastandvektori eeldusel, et $\vec{A B} ∦ \vec{a} .$ Punktiks P võib võtta ükskõik kumma punktidest A või B.

$\vec{A Q} =$ (x–x₁; y–y₁; z–z₁) ja $\vec{a},$ $\vec{b}$ ning $\vec{A Q}$ on komplanaarsed. Kasutame kolme vektori komplanaarsuse tingimust kolmerealise determinanadi kujul:

$|\begin{matrix} x - x_{1} & y - y_{1} & z - z_{1} \\ a_{1} & a_{2} & a_{3} \\ x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \end{matrix}| = 0 .$

Märka

Võrrand sisaldab kahte rihivektorit ja kolmandat vektorit, mis on nendega komplanaarne, seega tasand on määratud punkti ja kahe vektoriga.

Kehtib reegel:

Kui tasand läbib punkti P(x₀; y₀; z₀) ja kahte mittekollineaarset vektorit,

$\vec{a} =$ (a₁; a₂; a₃) ja $\vec{b} =$ (b₁; b₂; b3),

siis selle tasandi võrrand on

$|\begin{matrix} x - x_{0} & y - y_{0} & z - z_{0} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}| = 0$ .

Võrrand on determinandi kujul ja selle saab teisendada üldkujule näiteks Sarruse reegli põhjal või mõne teise meetodiga.

Lahendus

Q(x; y; z) on suvaline punkt tasandil.
Üks rihivektor on (–1; 5; 5).
Teine rihivektor $\vec{M N} =$ (; ; ).
Koostame võrrandi punktiga M.

$|\begin{matrix} x - 2 & y + 4 & z - 1 \\ - 1 & 5 & 5 \\ - 3 & 7 & - 4 \end{matrix}| = 0$

Vastus

55x + 19y – 8z – = 0 on otsitav võrrand.

(1; 1; –4)
(4; 1; 1)
(–1; –1; 4)
(3; 3; –12)

Sobiv tasandi võrrand on

$|\begin{matrix} x - 2 & y - 2 & z + 1 \\ 1 & 1 & - 4 \\ 0 & 4 & - 4 \end{matrix}| = 0$
$|\begin{matrix} 0 & 4 & - 4 \\ 1 & 1 & - 4 \\ x - 1 & y - 1 & z - 3 \end{matrix}| = 0$

Võrrand on .

More like this

Kolm punkti

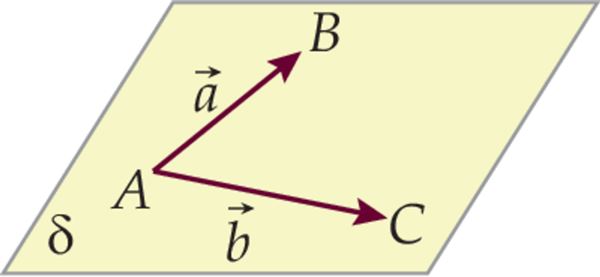
Kui on antud kolm tasandi punkti A(x₁; y₁; z₁), B(x₂; y₂; z₂ ) ja C(x₃; y₃; z₃), siis võtame rihivektoriteks mingid kaks vektorit, mis ühendavad neid punkte. Näiteks $\vec{A B}$ ja $\vec{A C}$ .

Võtame tasandil suvalise punkti Q(x; y; z). Saadud vektorid on mittekollineaarsed, sest eelduse kohaselt ei asu punktid ühel sirgel. Punktiks P võib võtta mis tahes punkti kolmest punktist A, B või C.

Kasutame kolme vektori komplanaarsuse tingimust kolmerealise determinanadi kujul:

$|\begin{matrix} x - x_{1} & y - y_{1} & z - z_{1} \\ x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ x_{3} - x_{1} & y_{3} - y_{1} & z_{3} - z_{1} \end{matrix}| = 0 .$

Võrrand on determinandi kujul ja selle saab teisendada üldkujule näiteks Sarruse reegli põhjal või mõne teise meetodiga.

Märka

Võrrand sisaldab kahte rihivektorit ja kolmandat vektorit, mis on nendega komplanaarne, seega tasand on määratud punkti ja kahe vektoriga.

Kehtib reegel:

Kui tasand läbib punkti P(x₀; y₀; z₀) ja kahte mittekollineaarset vektorit,

$\vec{a} =$ (a₁; a₂; a₃) ja $\vec{b} =$ (b₁; b₂; b3),

siis selle tasandi võrrand on

$|\begin{matrix} x - x_{0} & y - y_{0} & z - z_{0} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}| = 0 .$

Lahendus

Q(x; y; z) on suvaline punkt tasandil.
Rihivektoriteks sobivad

$\vec{A B}$
$\vec{A C}$
$\vec{B C}$
$\vec{B A}$
$\vec{C A}$
$\vec{C B}$

Võrrandisse on vaja neist valida mittekollineaarset vektorit.
Koostame võrrandi punktiga A ja vektoritega $\vec{A B}$ ja $\vec{A C} .$

$|\begin{matrix} x - 2 & y - 3 & z - 1 \\ - 1 & 0 & - 4 \\ - 3 & - 1 & 1 \end{matrix}| = 0,$

Vastus

–4x + 13y + z – = 0 on otsitav võrrand.

Vihje

Alati on hea harjutada võrrandi koostamist, aga mõelda tasub siiski:
1. Kui vabalt valitud kolmikuga koostatud võrrandisse sobib teine kolmik ⇒ ...(mitmes) langeb valikust välja.
2. Kui vabalt valitud kolmikuga koostatud võrrandisse ei sobi teine kolmik ⇒ ...(mitmes) langeb valikust välja.

A(3; 3; –1), B(10; 2; 2),
C(13; –1; 5)
K(2; 2; 2), L(–13; 5; –1),
M(4; 1; 2)
R(–1; 2; 1), S(9; 0; 3),
T(–5; 4; 1)

1)
2)
3)

Võrrand on = 0.

More like this

Harjuta ja treeni

$- z - 7 = 0$
$3 x + 5 y - 6 z + 5 = 0$
$7 x - 12 y + 13 z - 9 = 0$
$23 x - 40 y - 38 z + 154 = 0$

A(–3; 2; 1), B(2; –1; 1), $\vec{c}$ = (–1; 3; 2)
Tasandi võrrand on
A(1; 2; 2), B(3; 1; 0), C(–2; –3; –1)
Tasandi võrrand on
A(3; 4; –7), $\vec{b}$ = (0; 1; 0), $\vec{c}$ = (1; 0; 0)
Tasandi võrrand on
A(10; 2; 8), B(0; 1; 3), C(2; 5; 0)
Tasandi võrrand on

$2 x - y + 2 z - 11 = 0$
$13 x + 14 y + 17 z - 66 = 0$
$23 x - 40 y - 38 z - 154 = 0$
$3 x - 11 y - 5 z - 20 = 0$

A(3; –1; 0), $\vec{a} =$ (2; 1; –1), $\vec{b} =$ (–5; 0; –3)
Tasandi võrrand on
A(–1; 2; 3), B(2; –2; 4), C(1; 5; –1)
Tasandi võrrand on
A(1; –1; 4), $\vec{a} =$ (0; 2; 1), $\vec{b} =$ (1; 2; 0)
Tasandi võrrand on
A(10; 2; 8), B(0; 1; 3), $\vec{a} =$ (2; 4; –3)
Tasandi võrrand on

Antud tasandi normaalvektor $\vec{n}$ on otsitava tasandi

Võrrandisse sobivad komplanaarsed vektorid on

(1; 1; 1)
(0; –1; 1)
(–2; 1; 1)
(–4; –3; 6)
(4; 3; –6)
(3; 0; 4)
(x + 2; y – 1; z – 5)
(x – 2; y – 4; z + 1)
(x + 2; y + 4; z – 1)
(x – 1; y – 1; z – 1)

Vastus

More like this

Mõisted

Kaks tasandil või paralleelsel tasandil asuvat vektorit moodustavad selle tasandi

Iga vektor tasandil omab pikkust, suunda ja

More like this

Service provided by Star Cloud LLC

Join Opiq

Opiq score

	Tasks
	Chapter is studied

Tasandi võrrand rihi kaudu

More like this

Komplanaarsed vektorid

Märka

More like this

Punkt ja kaks vektorit

Lahendus

Vastus

More like this

Kaks punkti ja vektor

Märka

Lahendus

Vastus

More like this

Kolm punkti

Märka

Lahendus

Vastus

Vihje

More like this

Harjuta ja treeni

Vastus

More like this

Mõisted

More like this

Add content

Files to be added

Report Mistake

Only report errors related to the functionality or content of Opiq. Please describe the error as precisely as possible.

If you agree to share additional info, add your contact data (e-mail, phone).

Check to help us fight spam

Opiq uses cookies