Vaatleme mõningaid logaritmide omadusi. Tuletame seejuures meelde, et logaritmi saab leida vaid positiivsest arvust, mis tähendab, et järgmised seosed kehtivad vaid positiivsete logaritmitavate korral.
TEOREEM 1.
Korrutise logaritm võrdub tegurite logaritmide summaga, s.t
loga N1N2 = loga N1 + loga N2.
Tõestus.
Olgu loga N1 = r1 ja loga N2 = r2.
Siis
Logaritmi definitsiooni põhjal saame võrdusest
Näide 1.
Arvutame log 200, kui on teada, et log 2 ≈ 0,3010. Et 200 = 2 · 100, siis
log 200 = log (2 ⋅ 100) = log 2 + log 100 ≈ 0,3010 + 2 ≈ 2,3010.
TEOREEM 2.
Jagatise logaritm võrdub jagatava ja jagaja logaritmide vahega, s.t
.
Tõestus.
Olgu loga
N1 = r1 ja
loga
N2 = r2, s.t
Logaritmi definitsiooni põhjal saame võrdusest
Näide 2.
Arvutame log 0,0002, teades, et log 2 ≈ 0,3010. Et 0,0002 = 2 : 10 000, siis
TEOREEM 3.
Astme logaritm võrdub astendaja ja astme aluse logaritmi korrutisega s.t
loga
Nc = c loga
N.
Tõestus.
Olgu
loga
N =
r, siis
Näide 3.
Arvutame
Saadud valemeid kasutatakse ka avaldiste logaritmimisel, s.t avaldiste logaritmide avaldamisel neis esinevate suuruste logaritmide kaudu.
Näide 4.
Logaritmime avaldise y alusel a, kui
Näide 5.
Arvutame avaldise 4u4v5 kümnendlogaritmi, kui on teada, et log 2 ≈ 0,301, log u = 2,5 ja log v = –3.
Näide 6.
Lahendame eksponentvõrrandi 3x = 23,5.
Logaritmime antud võrduse mõlemaid pooli alusel 10:
Avaldise logaritmi või arvu logaritmi järgi vastava avaldise või arvu leidmist nimetatakse potentseerimiseks. Seejuures tuleb logaritme sisaldavate avaldiste teisendamisel kasutada tuletatud valemeid n-ö tagurpidi.
Näide 7.
Leiame arvu x, kui log9 x = 2,5.
Arvu x leidmiseks potentseerime võrdust log9 x = 2,5. Tulemusena saame, et x = 92,5 ehk x = 35 = 243.
Näide 8.
Leiame avaldise z, kui
Avaldise z leidmiseks teisendame antud võrduse paremat poolt:
Võrduse
Näide 9.
Aastatel 1970–2006 kasvas Aafrika rahvastik keskmiselt 2,62% aastas ja oli 2006. aastaks 925 miljonit. Leiame, mis ajaks kahekordistub Aafrika rahvaarv.
Et rahvastik kasvab liitprotsendilise kasvamise seaduse järgi, siis
925 ⋅ (1 + 2,62 : 100)n = 2 ⋅ 925, millest 1,0262n = 2.
Logaritmime võrdust alusel 10: log 1,0262n = log 2. Kasutades astme logaritmi omadust, on n ⋅ log 1,0262 = log 2 ja n = log 2 : log 1,0262 ≈ 26,8. Seega kahekordistub Aafrika rahvaarv, võrrelduna 2006. aastaga, aastal 2033.
Ülesanded A
Ülesanne 633. Avaldise logaritmimine
Ülesanne 634. Arvutamine
Ülesanne 635. Arvutamine
Arv | Arvu kümnendlogaritm |
19,5 | |
195 | |
1950 | |
19 500 |
Arv | Arvu kümnendlogaritm |
0,195 | |
0,00195 | |
1,95 ⋅ 10–10 | |
19,55 |
Ülesanne 636. Potentseerimine
Ülesanne 637. Logaritmvõrrandi lahendamine
Ülesanne 638. Euroopa ja Aasia rahvaarv
Ülesanne 639. Autoostu raha kogumine
Vastus. Joosep saab selle auto osta aasta pärast.
Ülesanne 640. Auto pidurdustee
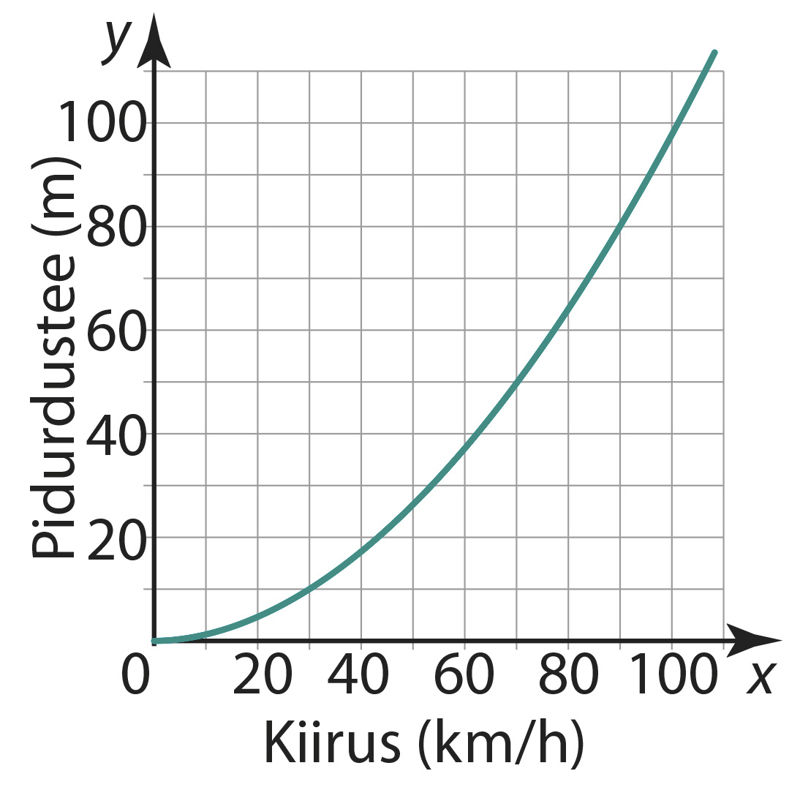
Vastus. a = , b =
y =
Arvutage auto pidurdustee pikkus täismeetrites, ümardades tulemuse ülespoole lähimaks 5-ga või nulliga lõppevaks arvuks, kiiruste 45 km/h, 65 km/h, 95 km/h, 120 km/h korral ja võrrelge tulemusi jooniselt saadavatega.
Vastus. Kiirusel 45 km/h on auto pidurdustee pikkus m; kiirusel 65 km/h m; kiirusel 95 km/h m; kiirusel 120 km/h m.
Ülesanne 641. Vee jahtumine

- Kujutage tabeli andmete põhjal jahtuva keha temperatuuri ja aja vaheline seos graafiliselt.
- Eeldades, et kõnealune seos avaldub kujul T = ae–bx, kus muutuja x on aeg ja T temperatuur, leidke parameetrid a ja b.
Vastus. a = °, b = - Arvutage vee temperatuur, kui nõu koos veega on jahtunud 2; 15; 43; 50 minutit.
Vastus. Kui nõu koos veega on jahtunud 2 minutit, siis on vee temperatuur °; kui 15 minutit, siis °; kui 43 minutit, siis °; kui 50 minutit, siis °.
Ülesanded B
Ülesanne 642. Avaldise logaritmimine
Ülesanne 643. Arvutamine
Ülesanne 644. Eksponentvõrrandi lahendamine
Ülesanne 645. Eksponentvõrrandi lahendamine
Ülesanne 646. Tõestamine
Ülesanne 647. Tõestamine
Positiivsete arvude x1, x2, …, xn geomeetriline keskmine defineeritakse valemiga
Tõestage, et antud arvude logaritmide aritmeetiline keskmine võrdub nende arvude geomeetrilise keskmise logaritmiga.
Ülesanne 648. Geomeetriline keskmine
Antud arvud | Geomeetriline keskmine |
240; 540 | |
8; 27; 125 | |
18; 49; 84 | |
2; 6; 9; 12 |
Ülesanne 649. Tõestamine
Tõestage, et a2 + b2 = 7ab, kui
Ülesanne 650. Tõestamine
Tõestage, et
Ülesanne 651. Autode pikivahe

Vastus. Maksimaalne kiirus võib olla ligikaudu km/h.
Ülesanne 652. Bakterite paljunemine
Vastus. k = . Bakterite mass kahekordistub tunni pärast.
Ülesanne 653. Pinnase kaldenurga ja puidukoguse vaheline seos

Eeldades, et pinnase kaldenurga x ja puidukoguse y vaheline seos avaldub kujul y = axb + c, leidke parameetrid a, b ja c.
Vastus. a =
Arvutage saadav puidukogus pinnase kaldenurkade 8°, 15°, 30°, 42°, 50°, 55°, 60° korral.
Pinnase kaldenurk | 8° | 15° | 30° | 42° | 50° | 55° | 60° |
Puidukogus |
Ülesanne 654. Ahvenad ja särjed
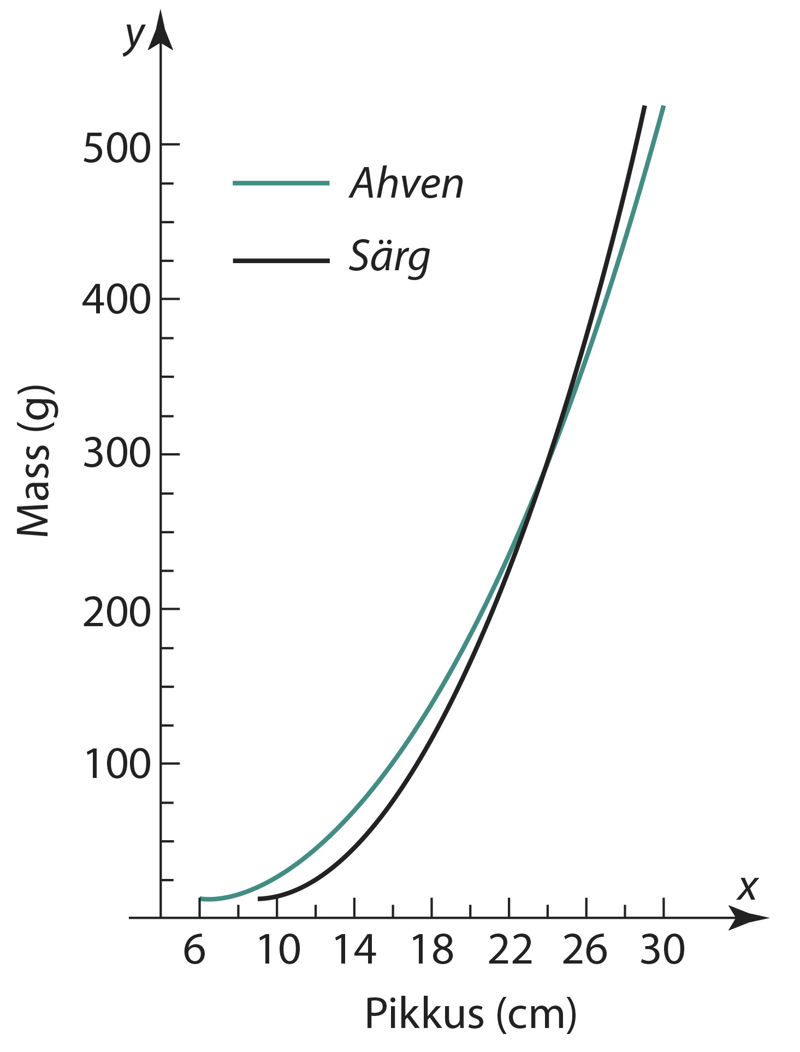
Joonis pärineb M. Kanguri artiklist „Kala pikkuse ja kaalu vahelisest seosest”, „Eesti Loodus”, 1970, nr 7, lk 445.
Vastus. Ahvena korral a = , b = ja särje korral a = , b = .
- Arvutage kala mass, kui kala pikkus on 15 cm; 28 cm.
Vastus. 15 cm pikkuse ahvena mass on grammi ja särjel grammi. 28 cm pikkuse ahvena mass on grammi ja särjel grammi.
Ülesanne 655. Ahvenad ja särjed

Joonis pärineb M. Kanguri artiklist „Kala pikkuse ja kaalu vahelisest seosest”, „Eesti Loodus”, 1970, nr 7, lk 445.
Vastus. Ahvena korral a = , c = ja särje korral a = , c = .
- Arvutage kala mass, kui kala pikkus on 15 cm; 28 cm.
Vastus. 15 cm pikkuse ahvena mass on grammi ja särjel grammi. 28 cm pikkuse ahvena mass on grammi ja särjel grammi.
